 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| トップ物理教育情報教育GPS考古学 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 GPS考古学のための初等解析幾何学はじめに私が名付けた「GPS考古学」は未開拓の分野ですが、やみくもにGPSを使えば何らかの成果が得られるものではありません。最初に研究対象がGPS測定に適しているか否かを判断することが大切です。 成果が期待できるものとしては、広域の地理的尺度を持つ対象物が考えられます。従来、精密な地図・地形図を使って調べていた事柄をより精度の高い数値測定で置き換える(あるいは補う)ものと考えたらよいでしょう。 丁度「アナログ」を「デジタル」に変える作業に相当します。 その利点は精度が上がること(例えば2万5千分の1の地形図の精度を1mmとすれば、誤差は25mになりますが、GPSではその約1/10の誤差で測定出来ます。).、データは数値化されているので分度器、コンパス等を用いた、更に誤差を呼び込む可能性のある作図をせず、計算で直接処理できることにあります。 ◎ 方位測定に威力 特に、旧来の方法に比較して、GPS計測の卓越した点は、直線の方位が正確に得られることです。従来の方位磁針による測定では、各地の地磁気の偏角の乱れ等があり、信頼性に欠けます。その点、GPSは地球座標に準拠しており、地磁気による方位のような基準の曖昧さはありません。GPSで正確な方位を得るには、基準線分の距離が長いことが要求されますが、たとえば2点間の距離が2km以上あれば、簡易GPS機器でも、約0.1度の精度で絶対方位が決定できます。それに比較して、羅針盤の目盛りでは1度以下の読み取りはそもそも不可能です。 ◎ 解析幾何学的計算が必須 もちろんGPS機器に直接方位が表示される訳ではありません。これらを得るには、座標を使った幾何学的計算が必要です。 このようにGPS計測ではすべて、解析幾何(座標幾何)を用いた計算が要求されます。 しかし、GPS考古学に関心を持たれている方の中には「理系」でない方も多いのではと想像されます。そこで以下に、GPS計測のために私が用いた基本的な解析幾何の式のいくつかを紹介しようと思います。 ただここでは、基本式を教科書的な通常の導出方法ではなく、私流に、簡便で直観的なベクトルの外積を用いる方法で紹介いたします。 ベクトルの外積について図のようにO点から2本の線分OA、OBが延びているとき、それぞれをベクトルとみなし、ベクトル 成分をそれぞれ (ax,ay), (bx,by) とし、また、ベクトルの大きさ(=長さ)をそれぞれ a、b とする。 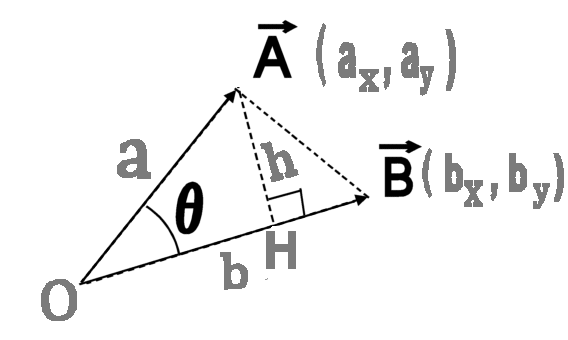 ベクトル で定義する。 ただし,±は (実際の外積の意味は、他にあるが、ここでは省略する。) この式の意味は図の三角形ΔOAB の高さ h が h = a sinθ であることに注目すると 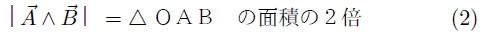
あるいはOA、OBを2辺とする平行四辺形の面積に等しいことが分かる。 ◎ 外積の性質 ・ 反交換 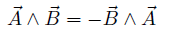 ・ 同じ向きのベクトルの積ゼロ 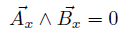 ◎ 外積の成分表示 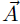 の成分を、(ax , ay)、 の成分を、(ax , ay)、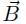 の成分を (bx
, by) とすると、 の成分を (bx
, by) とすると、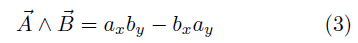 で表される。 互いに相手方の直交成分との積の和(向きが入れ替わると負になる)であることに注目。 なぜなら ベクトルを成分ベクトルの和とみなすと外積は 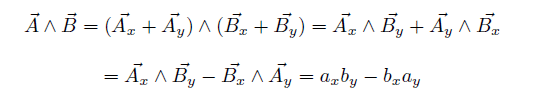 この関係式(3)は重要で、以下で多用する。 Ⅰ.デカルト座標での式GPSでは緯度、経度という尺度の異なる座標系を使うのですが、それへの変更は後に回して、まず x, y 座標軸が同じ尺度で直交する 所謂 「デカルト座標」 での式を導こう。 2点を通る直線の式図のように2点 A、B を通る直線の式を導こう。今、任意の点 P ( x, y ) がその直線上にあるための条件は、図の角 θ が sinθ = 0 となることである。 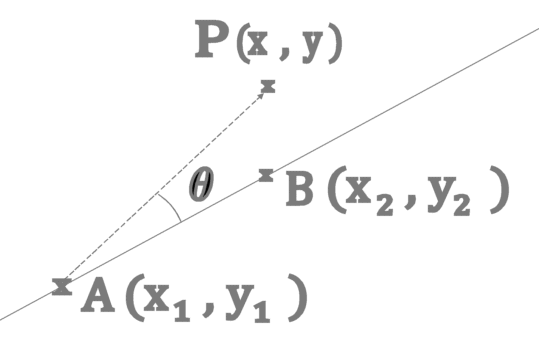 つまり、外積を使って表現すると 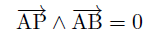
これを成分表示で表すと、 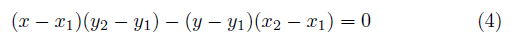 これが、2点 (x1,y1), ( x2 ,y2 ) を通る直線の式である。これを別の形に変形するとより分かり易いかも知れない。 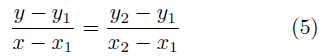 つまり、線分 AP と線分 AB の傾きが等しいことを表している。 あるいは、直線の傾きの角度を δと置くと、 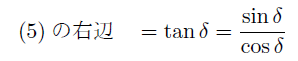 だから、 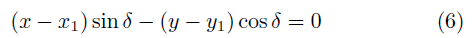
これが、点(x1 , y1) を通り、傾きの角度 δ の直線の式である。 (6)式は別解釈すると、(3)式を使って、ベクトル 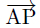 = (x-x1 , y-y1) と 単位ベクトル (cosδ , sinδ) の外積=ゼロ を表す式であると読める。 = (x-x1 , y-y1) と 単位ベクトル (cosδ , sinδ) の外積=ゼロ を表す式であると読める。直線の式の利用法1. 2点を結ぶ直線の延長線がどこを通るか。 直線の式は x , y の関係式だから、x が分かれば y が決まる。つまり、延長線が特定の経度を通過する点の緯度が計算できる。あるいは、特定の緯度を通過する点の経度が分かる。 たとえば、表計算ソフト等で、緯度の分、秒のセルにGPSの測定値を入れると、経度の分、秒のセルに自動的に計算結果を表示するように式を設定しておけば、GPSとPCを持ち歩いて延長線がどこを通るか追跡できる。 (パソコンは重いので、一番手軽なのは、所謂ポケコンである。 しかし残念なことに、現在入手できるのは、唯一シャープの教育用ポケコンしかないのは、なぜだろうか。) 2. 直線の方位が分かる。 2点が分かれば、線分の傾きから、その方位角が正確に分かる。 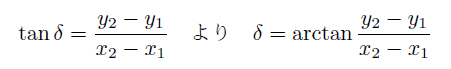 ただし、座標値 (x, y ) に経度、緯度を使うには、後で述べる変換係数α、βを掛ける必要がある。 直線からの垂直距離ある点Pが直線から、どれだけ離れているか知りたい場合がある。 図 のように、PからA点を通る直線に下ろした垂線の足までの距離 h は 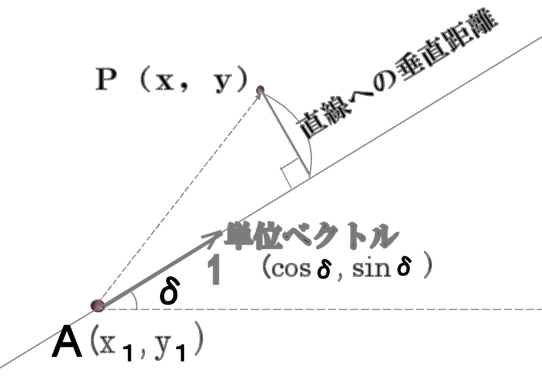 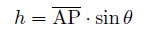 これは、ベクトル 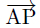 と直線の向きの単位ベクトル と直線の向きの単位ベクトル 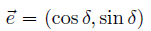 との外積に等しい。 との外積に等しい。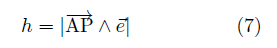
ここで、| | は、絶対値を表す。 座標値 P(x, y )、A(x1, y1)を使うと(7)式は 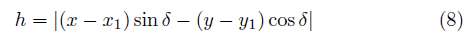
で与えられる。 (8)式の右辺は、上述の直線の式 (6)の左辺と同じものである! つまりP点が(6)式のゼロの値からずれている場合には、P点が直線から外れた距離を表す。 ただし、x , y等に、経度、緯度を使う場合は後で述べる変換係数を掛ける必要がある。 また、直線が角度でなく、線分ABで与えられて場合は、 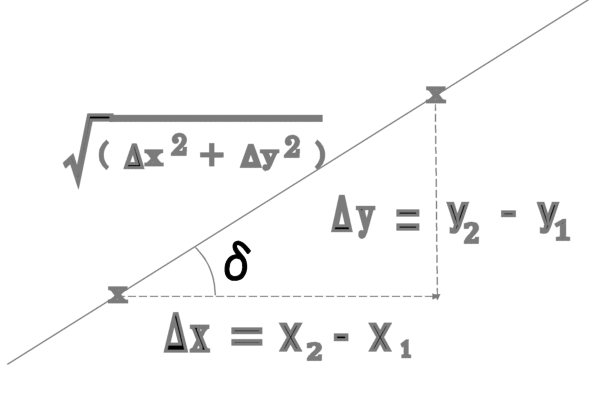 (8)式で 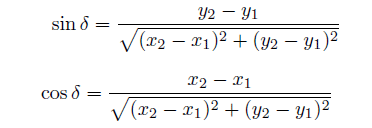 を使えばよい。ただし、経度、緯度を使う場合は変換係数α、βを掛ける必要がある。 2直線の交点を求める。図のように線分 AB の作る直線と線分 CD の作る直線の交点P の位置を求めよう。 C点から直線 AB までの垂直距離を h1、D点から直線 AB までの垂直距離を h2、 また線分 CD の長さを L とすると。 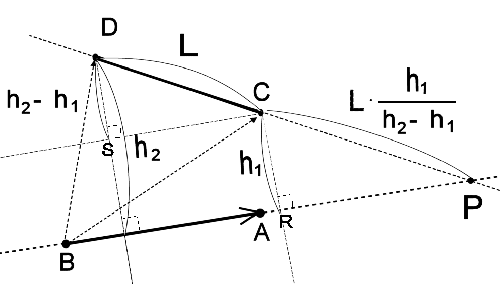 図の 三角形CDS と 三角形PCR が相似であることから、 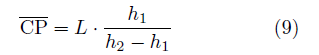
が得られる。 この h1, h2 をベクトル 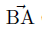 の向きの単位ベクトルとの外積で表現すると、 の向きの単位ベクトルとの外積で表現すると、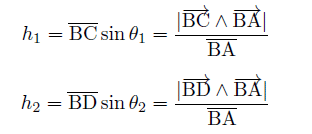
(9)式の 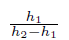 は分母分子に共通因子 は分母分子に共通因子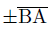 が含まれるので省くことが出来るので、 が含まれるので省くことが出来るので、代わりに外積 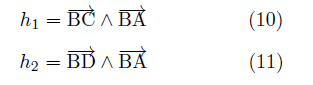
を用いて、 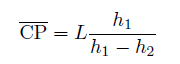
を計算すればよい。 たとえばP点の x 座標は C点、D点の x 座標 xc 、xdを用いて 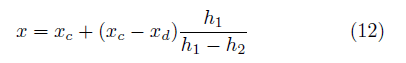 y 座標は同様に 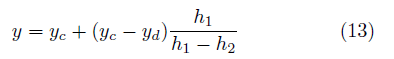 ここでh1、h2には、(10),(11)式を用い、その外積には(3)のような成分計算値を使う。 また交点の計算は x,y に経度、緯度を変換係数を掛けることなく、そのまま使うことができます。 2線分の成す角図のように、線分OA、OB の長さを a,b とし、成す角を θとする。 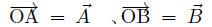 と置き、ベクトルの成分を と置き、ベクトルの成分を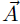 =(ax,ay) , =(ax,ay) ,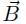 =(bx,by) とする。 =(bx,by) とする。ベクトルの成分から、その挟む角を求めるには、 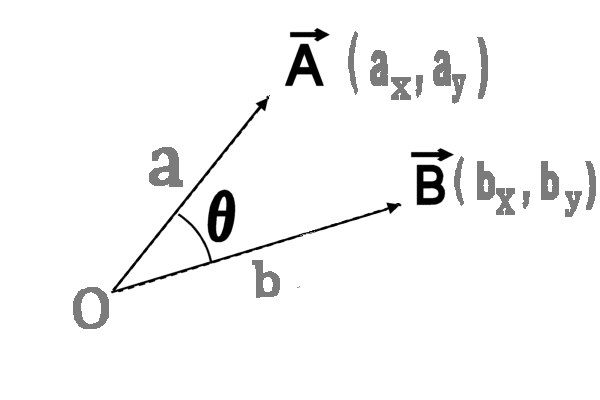 ◎ ベクトル内積を使う方法 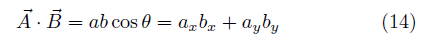 より、 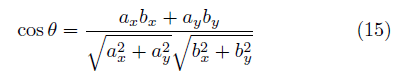 これから、θ は (15)式の arccos を計算すればよい。 ただし経度、緯度を用いる場合は変換係数を掛ける必要がある。 ◎ ベクトル外積を使う方法 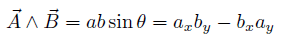 より 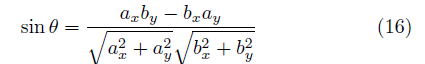 より、角θは角の向きに±があるので、 θ= | arcsin(16) | を計算すればよい。ただし、経度、緯度を使う場合は次に述べる変換係数を掛ける必要がある。 Ⅱ.緯度経度の長さ地球は球体(正確には自転の遠心力のため赤道方向に少し膨れた回転楕円体に近い球体)のため、経線の間隔は極に近づくほど狭くなる。つまり経度1度の長さが高緯度ほど短くなる。 また、緯度の間隔も回転楕円体のため曲率が一定でないので、若干緯度により変化する。 しかし、経線(南北線)と緯線(東西線)はどこでも垂直なので、我々の扱う局所的な範囲(地球面の切平面)では、軸の目盛が異なる直交座標系とみなして差し支えはない。 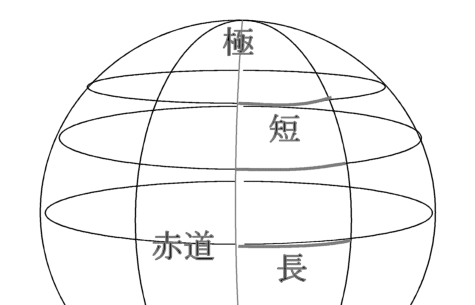 以下の計算式を導くのは本題ではないので、結果の式のみを示す。 赤道半径 a 、離心率 e 、緯度 φ として、 ・ 経度1秒の長さ α は(単位 m) 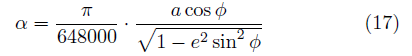 ・ 緯度1秒の長さ β は(単位 m) 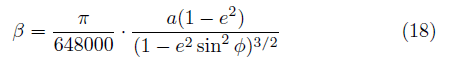 ここで、赤道半径 a = 6378137m、(離心率)2 e2 = 0.006694470 、φ = その地の緯度 、を使って計算すればよい。 αは緯度に敏感であるが、βは緯度に鈍感である。 これらの計算はPC上で表計算ソフトか簡単なプログラム言語を使うか、またはポケコン、関数電卓等を用いて行えばよい。 デカルト座標(x,y)の代わりに経度、緯度を使うには・経度、緯度を秒単位に直す。 まず、調べたい地域の座標原点(0, 0)を決める。 通常、横軸 x 軸は経度(東に行くほど値が増す)を、縦軸 y 軸は緯度(北に行くほど値が増す)をとり、 それぞれ度の部分を省いて、分、秒の部分のみを使うと良い。さらに分を60倍して秒に直して、経度、 緯度とも秒単位に直す。 ・調べる地域の経度、緯度の1秒の長さを計算する。 上述の (17), (18)を用いて、変換係数 α、β を求める。 ある点の(経度、緯度)が秒単位に直して、( k ,i ) なら 座標値 (x , y) = (α k ,β i ) になる。 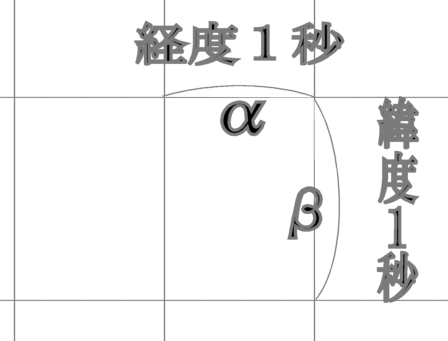 この変換を行えば上述のデカルト座標のすべての式が使える。 ただし(4),(5),(9),(12),(13)は変換なしで、(x , y) = (経度、緯度)で使用可能である。 [参考] 以下に、北緯 34度付近の α、β 計算値を示す
Ⅲ. 最小2乗法上では、直線が2点から正確に決定できる、あるいは、1点とそれを通る直線の向きが正確に分かっていると云う条件のもとで、直線の式を求める方法を議論をしてきた。 しかし、「筋違道」の例のように直線の痕跡と思われる場所が点々と残っているがそれらが正確かどうか分からないと云った場合には上述の方法では直線の式を求められない。 この場合、誤差を含む多数の点から元の直線を統計的に推測する必要があります。 私が「筋違道」の場合に採った方法は「最小2乗法」です。 つまり、直線からの誤差(ずれ)の大きさの2乗平均ができるだけ小さくなるような直線の式を求める方法である。 ◎ 統計処理の注意 まず、こう云った統計的方法を使うに当たっての注意を述べておく事は重要であろう。 ① 本当に直線であるかの見極め。 もともと直線でないものに適用しても誤った結論が出るだけである。 ② 本当に直線であると考えるなら、直線が確実に通ったと思われる場所を探し出すことが先決であり、あやふやな多数の場所を含めた統計的処理は避けるべきである。 ③ 明らかに直線から大きくずれていると思われるデータは除外すべきである。 誤って大きくずれた点を含めてしまうと計算結果に大きなくるいが出る。 ④ 数学や数字にだまされない。 「多数のデータをとれば、信頼できる値がえられる。」 「数学的計算結果であるから厳密な値である」であると考えるのは、確率・統計処理に限っていえば正しくない。 結果の数値は判断材料の1つと考えるべき。 真実は一つであるので他のアプローチからの確認、突き合わせが大切である。以上を踏まえた上で利用を願いたい。 ◎ 最小2乗法の導出 図のように、n個の測定データ (x1,y1),(x2,y2) .. (xi,yi) .. (xn,yn) が与えられているとする。それらのほぼ中央を通る直線の式、  を求めたい。 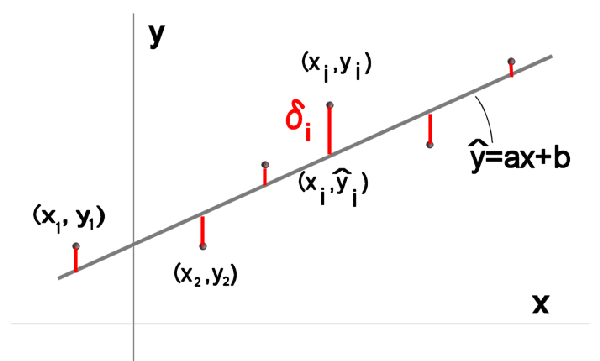 仮に(20)式を仮定して、その直線からの誤差δの2乗の和 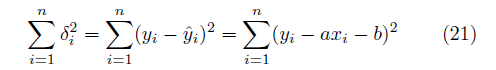
を最小にする a , b の値を求める方法を最小2乗法という。 (21)を2変数 a, b の関数とみなし、 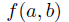 と置く。 と置く。この関数 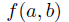 が最小になる条件は、変数 a, bそれぞれに関する微分がゼロ が最小になる条件は、変数 a, bそれぞれに関する微分がゼロ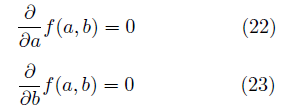
である。 (22)より 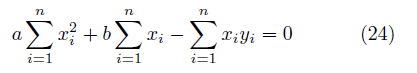
(23)より 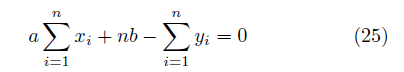
を得る。 ・結論 (24),(25)を連立させて、 a, b を求めると、 傾き a は 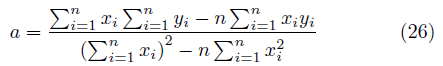
直線の y 軸切片 b は、 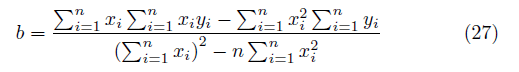
を得る。 処理はデータ xi, yi を表計算ソフトに入力して、(26) (27) の計算行うとよい。 (註) 単に直線の式のみを得たい場合は x、y に経度、緯度を使ってよいが、傾きの角度を得たい場合は、傾き a だけは、α、βを使って、実の傾きに直さねばならない。 |
GPS考古学初期巨大古墳の方位規則性と王位継承仮説New! 箸墓古墳と夏至の太陽 New! 太子道・筋違道の研究 ご感想等 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||