 |
|
| �g�b�v������������f�o�r�l�Êw | |
 �����͂ɂ��Ă̑Θb�@�i�P�j�h�����͂͌������̗͂ł͂Ȃ��h�E���_�@�Θb���璷�Ɏv������́A�K�X�Ƃ��ǂ݂��ĉ������B�d�v�Ș_�|�͌㔼�����B �@�܂��A�v����h��������̃y�[�W�̉��h�ɂ���܂��B �z�[���Y�F�@���g�\���搶�A����ɂ��́B ���g�\���F�@�₠�A�z�[���Y�N�A�v���Ԃ肾�ˁA����ȂƂ���ʼn���Ƃ́B�ǂ����Ă�H �z�[���Y�F�@���A��w�ɒʂ��Ă��܂��B���Z�𑲋Ƃ��Ă���搶�ɂ������̂́A���߂Ăł��ˁB �@�����́A�V�C���ǂ��̂ŁA�Ԃ���ƎU�����Ă�����ɗ����Ƃ���ł��B ���g�\���F�@�������B�N����w�����B �z�[���Y�F�@�Ƃ���ŁA�ŋ߁A�搶���l�b�g�Ƀz�[���E�y�[�W�����ꂽ�̂����킳�ŕ����āA�ǂ܂��Ă��������܂����B ���g�\���F�@�����A�ǂ�ł��ꂽ�̂��A���肪�����B�܂��A�N�Z�X�������Ȃ��č����Ă����Ƃ��낾�B �z�[���Y�F�@���́A�����͂̂Ƃ���ŁA�܂��D�ɗ����Ȃ��_������̂ł����B ���g�\���F�@�����Ȃ��A���ł������Ă���B �z�[���Y�F�@�搶�́u�����݂͂͂����̗͂ł͂Ȃ��v�ƌ����Ă���̂ł����A��͂�A�u�݂����̗́v�ł�����悤�Ɏv���̂ł��B �@�Ⴆ�A�����[�S�����h�̂悤�ɉ�]����ꏊ�ɂ���l���{�[�����܂������O���ɓ������Ƃ���ƁA�{�[���͂܂������ɔ��ōs�����ɋȂ����ĉ^������悤�Ɍ����܂��ˁB ���g�\���F�@�������ˁB�������A�d�͂ʼn��ɋȂ��邱�Ƃ������Ă���̂ł͂Ȃ����낤�ˁB �z�[���Y�F�@�Ⴂ�܂���B�ܘ_�A���d�͂̉e�����Ȃ��ƍl���Ă̘b�ł���B���ɋȂ����ċȐ���`���悤�ɔ��ł����悤�Ɍ�����ł��傤�B ���g�\���F�@�����A���������邾�낤�ˁB �z�[���Y�F�@�{�[���͂����͂����ɂ܂������i��ł���ɂ��S�炸�A�ϑ��҂���]���Ă��邽�߂ɁA�����ɑ��đ��ΓI�Ƀ{�[�����Ȃ����ĉ^�����Ă���悤�Ɍ����邾���ł���ˁB ���g�\���F�@���̒ʂ肾�ˁB �z�[���Y�F�@������~�^������܂�����x�n�ɂ���ϑ��҂��猩��ƁA�{�[���ɉ��S�͂�R���I���̗͂̂悤�Ȋ����͂������悤�Ɍ����邩��A�Ȃ����ĉ^������Ƃ������Ƃł��ˁB �i�@�R���I���̗͂ɂ��ẮA�ʃy�[�W�u�R���I���̗͂ɂ��āv���Q�Ɓ@�j ���g�\���F�@�����������Ƃ��ˁB �z�[���Y�F�@�������A�{���͂���ȗ͂Ȃ�ē����Ă��Ȃ��ł��傤�B�{�[���͂����܂��������ł��邾���Ȃ���B ���g�\���F�@���̒ʂ肾�B �z�[���Y�F�@��������A���S�͂Ƃ��R���I���̗͂Ƃ��͂����܂Łu�������̗́v�ł����āA�����̗͂łȂ��ƌ�����̂ł͂Ȃ��ł��傤���B�搶�̃y�[�W�ł́A�u�����͂͌������̗͂ł͂Ȃ��B�����ɑ��݂���͂��v�Ǝ咣����Ă��܂������B ���g�\���F�@���[��A�Ȃ�قǁB�Q�����ȁB�m���ɁA�{�[���ɂ͂���ȗ͓͂����Ă��Ȃ��B�E�E�E ���炭�l���Ă����Ă���B�E�E�E �@����A�����l������ǂ����낤���B �z�[���Y�F�@�͂��A�����������Ă��������B ���g�\���F�@�b�͂������B�����͓��m�ł����������āA�����͂͊��S�ɑł��������̂ŁA�����̗͂Ƃ��Ă����݂��Ȃ��̂��ƁB �z�[���Y�F�@�ǂ��������Ƃł����H ���g�\���F�@�����x�n�ł����]�n�Řb�����悤�B�{�[���ɂ́A�Q�̊����͂��t�����ɓ������ƂɂȂ�B �P�͉��S�͂�R���I���͂̂悤�ȗ́A���ꂪ�^���������̊O�͂ɑ�������B �@�����P�͎��̊����͂̃y�[�W�ŏЉ�������R�͂ɑ������銵���́A�܂�����x�n���猩��ƃ{�[���͉����x�^�����Ă���悤�Ɍ����邩�炻�̉����x���Ƌt�����ɓ����A�@�e�f�@���|�����̊����͂��B �@���̂Q�̗͂͂ǂ�������������͂ő傫���������������͋t������A�^�̈Ӗ��őł����������A�͂͏��ł���B���ǃ{�[���ɂ͑S�������͓͂����Ă��Ȃ����ƂɂȂ�B �@��ʂ̊O�͂̏ꍇ�ɂ������R�͂ƊO�͂��荇�����A�Q�َ͈��ȗ͂̂��߂Ɍ��ʂƂ��Ă荇�������Ȃ̂����A���̏ꍇ�ɂ͓�����ނ̊����͓��m�ł���̂ŁA���S�ȈӖ��ŐՌ`�Ȃ������Ă��܂��B �@���傤�Ǐd�͒��ł̎��R�����̏ꍇ�̖��d�͏�ԂƓ��l�A�����I�ɗ͂͏��ł���Ƃ����킯���B �z�[���Y�F�@�Ȃ�قǁA�Ȃ�ƂȂ����������悤�Ɏv���܂��B���̏ꍇ�A�{�[���ɂ͎��ۂɂ͂܂����������͓͂����Ă��Ȃ��Ƃ������ƂɂȂ�킯�ł��ˁB ���g�\���F�@�����������Ƃ��ˁB �z�[���Y�F�@���[��A�Ȃ�قǁB���ƂȂ��A���g�\���搶�̂�������Ă���u�����́v�̈Ӗ������������悤�Ɏv���܂����B�E�E�E�������A�E�E�E �����͂ɂ͔���p���������g�\���F�@ �܂������D�ɗ����Ȃ��_������̂��ȁB�z�[���Y�F�@�����A�b�������Ԃ����ƂɂȂ�܂����A���̗�ŁA�����͂Ƃ��āA�܂�搶�̌�����u�����̗́v�Ƃ��Ă������Ă��Ȃ��ƌ������Ƃ́A ��͂�����x�n�ł̉��S�͂�R���I���͂͌����ɂ͑��݂��Ȃ��A�܂��Ɂu�݂����̗́v���ƌ����Ă��邱�ƂɂȂ�܂��B ���g�\���F�@���[��A�������A�����Ȃ邩�B �z�[���Y�F�@���������āA�搶�̌�����u�����́v�Ƃ́u�����x�n�v�ł̋c�_�ɓo�ꂷ�邻��ł͂Ȃ��A�u�����n�v�ʼn����x�^�����镨�̂ɓ����u�����́v�̂��Ƃł͂Ȃ��ł����B ���g�\���F�@����A�������B���̒ʂ肾��B �@�킵���A�B���������_�ɋC�����āA�悭�w�E���Ă��ꂽ�B�������́A�z�[���Y�N��������B �@�N������������́A�����n�Ō���ƁA�P�ɊO�͂����ɓ����^�������Ă��镨�̂��A��]�n�i�����x�n�j�̊ϑ��҂��璭�߂��ꍇ�̗Ⴞ����A�����n�ł͉����x�[���Ȃ̂ŁA�킵�̉]���h�����́h�������Ă��Ȃ��B�܂�h�݂����̗́h���Ɖ]����킯���B �@���ꂶ��A�����n�Ō��Ă��A�����x�^�����Ă���ꍇ�͂ǂ��Ȃ邩�ˁB �z�[���Y�F�@�@��]�n�͘b�����G�ɂȂ�̂ŁA�P���ȗ�A�搶���u�����͂̕W���I�����v�̃y�[�W�ł������u�l���n�����R���đ���ꍇ�v���ɂ�����ƁA�����n�ł̖{���̐}�͂����Ȃ�܂��B�i���}�j�@�������n���̉�]�͖����B �@�@ 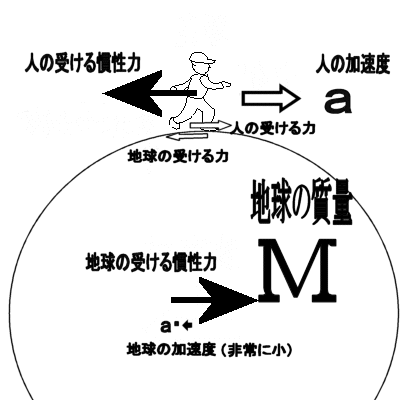  �@�@�@�@�@�@�@�@�@�����n�ł̐}�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����x�n�ł̐} �l�̏R�����͂��@�|���@�Ƃ���ƁA���̔���p�́@�{���@�̑O�����̗͂�l�͎�̂ŁA �����x�́@���@���@���^���@�ł�����A�����͂͌������@�|�����@���Ȃ킿�@�|���~�i���^���j�@���@�|���@�ɂȂ�܂��B �n���̕��́@�|���@�Ł@�R����̂ŁA���l�̌v�Z�i���@���@�l�@�ɑ��邾���j�ŁA�O���������́@�{���@���������ƂɂȂ�܂��B�@ ���g�\���F�@�������ȁA�Q�̊����͂́A�傫���������������͋t�A�܂�݂��ɁA��p�E����p�̊W�����藧�B����́A���������{���̗��̏؋��ł�����B �z�[���Y�F�@�Ƃ��낪�A��������l����ɂ����h�����x�n�h�ł́A�E�}�̂悤�ɁA�n���́@�|�l���@�̊����́E�E�E�����ƊԈ�����E�E�u�݂����̗́v����悤�ɂ݂���B �@����ȑ傫�ȗ͂������͂��͂Ȃ��ł��ˁB ���g�\���F�@���̒ʂ�B���̌������̗͂ŁA�n���͌��ɉ����x�@�|���@�ʼn�������ƌ�����B�@����ł��܂������Ɖ]���A�������b����B �@����ɁA���̗͂ɑΉ���������p�͂Ȃ��B �@���S�݂͂͂����̗͂ł͂Ȃ��@�z�[���Y�F�@�Ƃ���ŁA���S�͂͂ǂ��Ȃ̂ł��傤�B�@�悭���S�͂̋c�_�ŁA�����̐}�̂悤�ɁA�������ĉ~�^�������Ă��镨�̂̎����ƁA�~�̔��a�����ɔ��ōs�����A �ڐ������ɔ��ōs���̂ŁA���S�͎͂��ۂɂ͑��݂����A�h�݂����̗́h���B�Ɖ]���咣���悭���ɂ���̂ł����B���g�\���F�@�q�����܂��̂悤�Șb���ȁB�@�悭�l���Ă����A��������u�Ԃ���A���̒��͖͂����Ȃ�̂�����A���R�A���̊����R�͂ł��鉓�S�͂������ɖ����Ȃ��ŁA �Q�̗͂����Ƀ[���ƂȂ邩��A�����̖@���ɂ��A���̎��_�̉^���̌����A�܂�ڐ������ɓ����^������͓̂��R����B �@�@�@ 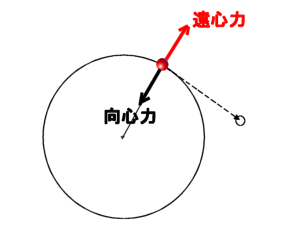 �@ �@ �@�@�@�@�@�@�@�@�@�@�������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��]����h�������̕��� �@�@�~�^�����镨�̂͌��S�͂ɂ���āA���̑��x�x�N�g���̌������A�~�̒��S�����₦���ω��������Ă���B�@���̕ω��i�������x�j�ɋt����Đ����������R�́i�������́j���h���S���h�ł���A�h�{���̗��h���B �@�{���Ɂh���S�͂������Ă���̂��A�ۂ��h��������̂́A���̂͗͂���ƁA�͂̂��ߑ����Ƃ��c�ނ킯�ŁA��������o����悢�B�E�̐}�̂悤�ɁA���x�́A��]����h�������Ƀ{�[�������āA������]������ƁA�ǂ��Ȃ邾�낤�B �@���������Ƃ��A����A�E��������@�Ōo�����Ă���̂ŁA���������邾�낤�B �z�[���Y�F�@�Ȃ�قǁA���́A�E�������ƁA�y�V�����R�ɂȂ�܂�����A���S�͎͂��݂���킯���B ���R�Ƃ����A���R�̘b�ł��ˁB �@�����P����ł����A����Ȃ�A���S�͂ɂ��A����p������͂��ł��ˁB����͌��S�͂̂��Ƃł��傤���B ���g�\���F�@����A�������߂ł��Ȃ����Ƃ��Ȃ����A�h�����́h�̔���p�́A��͂蓯�����h�����́h�ł���ׂ����B ��Ƃ��āA�f���^�����l���悤�B���L���͂ŁA���̐}�̂悤�ɁA���z�̂悤�ɏd�����̎�����y�������~��`���ĉ���ďꍇ���l���悤�B ������d�����Ɖ]���ǂ��A�f������̈��͂ŁA��������A�ӂ�ӂ�Ɠ��������B���̂Ƃ��A�����Ȃ��i���邢�͓����^������j�̂́A���z�ł͂Ȃ��A���z�Ƙf���Ԃ̏d�S�A���Ȃ킿�A���z�Ƙf�������Ԑ������A�����̎��ʂ̋t��ɓ�������_���B ����́A�^���ʕۑ����ŏؖ��ł���b���B ���̐}�ŁA���z�A�f���̎��ʂ��A�@�l�@�A���@�@�d�S����̋������A�@�q�@�A���@�Ƃ���ƁA �@�q�@�F�@���@���@���@�F�@�l�@�@�@�@�܂�@�@�l�E�q�@���@���E���@ �@�@�@�@�@�@�@�@�@ 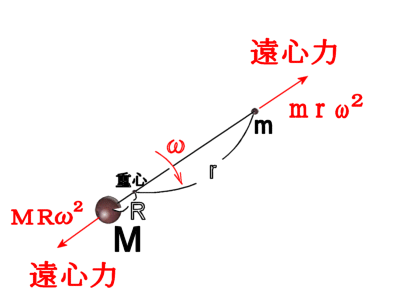 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�@�S �@��]�̊p���x���@���@�i���ʁj�Ƃ���Ɓ@�A���S�͂͂��ꂼ��@�l�E�q�E���Q�@�A�@���E���E���Q �@ ����́A��́@�@�l�E�q�@���@���E���@�@���g���Ɠ��������Ƃ�������B ���ǁA���̂Q�̉��S�͍͂�p�E����p�̊W�ɂ���Q�͂��B �܂�A�h���S�͂ɂ͔���p���Ȃ��A�U�̗͂ł���h�Ɖ]���̂͑S�������̂Ȃ��咣����B �z�[���Y�F�@�Ȃ�قǁB����E������Œ��A����@���K�^�K�^�h���̂́A���̔���p�̂������B ���g�\���F�@���Ԃ�A�������낤�B�܂����̎h���ŁA����@�����U���āA�U������������邱�Ƃ����邾�낤�ˁB �@ ���ׂĂ̊����͂ɂ͔���p������@�z�[���Y�F�@�Ȃ�قǂˁB�@�@����ł́A�ǂ�ȏꍇ�ł������͂ɂ͔���p������Ɖ]����̂ł��傤���B���g�\���F�@��������A������ƍl���Ă����B��ʓI�ɉ]���āA���̂`�����̂a����̊O�͂e���āA������������Ƃ��A�`�ɂ͊����R�́A���Ȃ킿���̉����x�ɑ���t�����̊����́i�|�e�j���������邪�A���̂Ƃ��a�͕K�������̏o�����͂̔���p�i�|�e�j���邩��A�a���t�����ɉ�����������i�܂�`���甽������j�̂ŁA�a�ɐ����銵���͂͂��傤�ǁ{�e�ƂȂ�B������ƌv�Z����킩��͂����B �z�[���Y�F�@���[��A�O�̊����n�Ō����n���������ĉ^�������Ɠ����悤�ɍl������悢�킯�ł��ˁB ���g�\���F�@���̒ʂ肾�B����́A�^���ʕۑ���������ۏႳ��邱�Ƃ��B �z�[���Y�F�@�ǂ��]�����Ƃł����B ���g�\���F�@�`�̉^���ʂ���1�u1�A �a�̉^���ʂ���2�u2�@�ƒu���ƁA�^���ʂ̘a�͕ۑ����邩��A �@�@�@��1�u1�{ ��2�u2�����A�E�E�E�E�E�E�E�@�� ��������Ԕ�������A�����x�����ŕ\���ƁA ��1��1�{ ��2��2���O�A �܂�@�|��1��1�� �|�i�|��2��2 �j�@�E�E�E�E�E�E�E�A�� ����͂`�A�a�̊����͂��݂��ɋt�����ő傫�������������Ƃ�\���Ă���B �z�[���Y�F�@�Ȃ�قǁA�{���̊����͂ɂ͔���p�����邱�Ƃ́A�^���ʕۑ����ŕۏႳ���̂��B�@ ���g�\���F�@�ʂ̕\��������A�����͂́A�ʏ�̕��̊Ԃ̑��ݍ�p�͂́h��h�i�傫�������������Ό����̗́j�Ƃ��Č���邩��A���ݍ�p�͊ԂŁh��p�E����p�̖@���h�����藧�ĂA���̑�ł��銵���͂̊Ԃł��h��p�E����p�̖@���h�����藧�B�i���Ƃ��@�}�@�S�@�Q�Ɓj �@����ɉ]���A�h�����͊Ԃ̍�p�E����p�̖@���h�Ƃ́A���ǁA�h�^���ʕۑ����h�̌��������ɂ����Ȃ��B�@�i��́@�A������@�@���@�����Ƃɑ�������B�j �z�[���Y�F�@���[��D�D�������B�D�D�D�Ȃ�قǂˁB �݂����̗͂Ɗ����͂̋���@�z�[���Y�F�@�@�Ƃ���ŁA�u�݂����̗́v �Ɩ{���̊����͂͂ǂ���ʂ���Ηǂ��̂ł����B���g�\���F�@��������悤�B�}�̂悤�ɁA�d�Ԃ̎ԓ��Ƀ��[����~���A���̏�Ƀl�R���悹����Ԃ�u�����Ƃ���B�܂��A���[���Ƒ�Ԃ̊Ԃ̖��C�͂���߂ď������Ɖ��肷���B�d�Ԃ������x���ŋ}���i������A�ǂ����낤�B �@�@ �@�@ 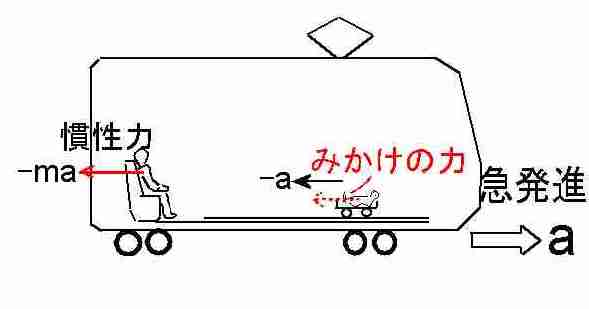 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�@�T ���R�A�}�̂�����ɍ����Ă����q�͒n�ʂɑ��āA�O���������x�@�{���@�ʼn������Ă��邩��A���������[�����@���{���̗͂ł����u�����́v��������ˁB �z�[���Y�F�@�O�y�[�W�̐搶�̐����ɏ]���ƁA�����Ȃ�܂��ˁB ���g�\���F�@��Ԃ̕��͂ǂ����B �z�[���Y�F�@���Ԃ�A���C���Ȃ��Ȃ�������ɁA�|���@�̉����x�œ����ł��傤�B�|�������ł��ˁB ���g�\���F�@���̂Ƃ��A��q�͂Ȃ���Ԃ��������ɉ��������̂��A���R���ǂ��������邾�낤�B �z�[���Y�F�@���Ԃ�A�������̗͂�����������A�Ɛ�������͂��ł��B ���g�\���F�@���̗͂́A�킵�̌����u�������v���u�݂����̗��v���A�ǂ������ˁB�����́h�l�R�h�ɕ����Ƃ悢�B �z�[���Y�F�@���[��A�Ȃ�قǁB�l�R�̓X���[�Y�ɓ�����Ԃɏ���Ă��邾��������A�n��ɑ��āh�Î~�h���Ă���̂Ɠ���������A�͂������Ȃ��͂��ł��ˁB�܂��u�݂����̗́v�Ɖ]�����ƂɂȂ�܂��B ���g�\���F�@������A�ȒP����B�n�ʁi�����n�j�ɑ��Ď��ۂɉ������Ă���Ȃ�A�����͂��邵�A�������Ă��Ȃ��Ȃ�A�݂����̗͂Ƃ������ƂɂȂ�B�@���̗�ŁA���[���Ƒ�Ԃ̊Ԃɖ��C������A���̗͂̏��ׂŁA��Ԃ͒n�ʂɑ��āA�����x�@�O�@�ł͂Ȃ��@�O���������x�@���f�@�i�@�����@�j�@�ʼn^�����邩��A����ɑ�������{���́u�����́@�v�@�|�����f�@���邾������B �z�[���Y�F�@�Ȃ�قǁB���̏ꍇ�̓l�R����̊����͂��������Ɋ����邱�ƂɂȂ�̂��B ���g�\���F�@�悵�A�����Ƃ͂����茾�����B �@���������A�����x�n�Ƃ́h���w�I�ȃg���b�N�h�ŁA�����Ŏg����̂��u�݂����̗́v�Ȃ�B �@����ɑ��āA�������̕��́A�����n�ł̉^���������@�e�|�������O�@���@�O�́@�e�@�Ɓ@�������ꂽ���̂ɐ�����t�����̗́i�������j�|�����@�̒ނ荇���̎����Ɖ��߂���Ƃ� �o�ꂷ����̂ŁA����́A�킵�����ǂ��Ǐq�ׂ��悤���^�̗����B �@�������̊����͂��u�j���[�g���͊w�v�ł͖��������u�v�ɂȂ��Ă���B���������u���z�̗��v�ł��邩�̂悤�ɂˁB �@������A���܂��܂ǂ�������������^���ɓo�ꂷ��A�u���z�̗��v���Ƃ��āA��������Ղ��̂��ƁB �@�����l������A�ǂ����ȁB �z�[���Y�F�@�Ȃ�قǂˁB �@�����A���搶�̌���ꂽ�h���w�I�g���b�N�h�Ɖ]�����t���C�ɂȂ�܂��B ���������������Ă��炦�܂��B �����x�n�Ɖ]�����\�@���g�\���F �ʔ����Ȃ��Ă������B���x�́A�z�[���Y�N�ɍl���Ă��炨���B�z�[���Y�F�@�����A�ڂ����l�����ł����B ���g�\���F�@�������A�킵�̎���ɓ����Ă���B �@���̂��Ƃ�[���l����Ƃ��́A�����ł��A�c�_�̏o���_�A�N���ɑk���čl����̂���{���B�@���������u�݂����̗́v�̋c�_�̏o���_�͉��������H �z�[���Y�F�@���[�ƁA�^�����u�����n�v�ł͂Ȃ��A�u�����x�n�v�łȂ��߂��Ƃ��Ɍ���Ă���u���z�I�ȗ́v�ł����ˁB ���g�\���F�@���̒ʂ肾�B���Ɂu�����n�v���猩�āA�����x�@��0�@�ʼn^������ꏊ���u�����x�n�v�̊�ɍ̂낤�B���A����^�����镨�̂��u�����n�v���猩�������x���@���@�A�u�����x�n�v���猩�������x���@���f�Ƃ���i���ׂđ����̓x�N�g���j�B �@�����̊W�́H�@�z�[���Y�N�B �z�[���Y�F�@���[�ƁA���@���@���f�{�@��0�@�@�ł��B ���g�\���F�@�������ˁB�悭�A�c�_������]�n�ł̊W���Ō����ƁA �@�@�@���@���@���f�@�{�@�Q�ց~���@�{�@�ց~�i�ց~���j �����Ł@���@�͐Î~�n����݂���]�n�̊p���x�A�@���@�͉�]�n���猩�����̂̑��x�A�@���@�͕��̂̈ʒu�x�N�g���i����͂ǂ��炩�猩�Ă������j�A�@�~�@�̓x�N�g���ς�\���A���B �@�����̐����͗͊w�̋��ȏ��ɍڂ��Ă���B�i�@��]�n�́@�R���I���̗́@�Ɓ@���S�͂̎��@�̓��o���@�ɂ��Ă��@�ʃy�[�W�u�R���I���̗͂ɂ��āv���Q�ƁB�j �z�[���Y�F�@�����A��w�̗͊w�̎��ƂŏK���܂������A��������̂������Ă��܂��B ���g�\���F�@�Ƃɂ����A �@�@�@���@���@���f�{�@��0�@�@�@�@�@�@�@�@(1) �@���B �z�[���Y�F�@���̕���������Ղ��ł��B ���g�\���F�@�����ŁA�u�݂����̗́v�͂ǂ̂悤�ɓo�ꂷ��̂��ȁB �z�[���Y�F�@��̎��̗��ӂɕ��̂̎��ʂ��������� �@�@�@�����@���@�����f�@�{�@����0�@�@�@�@�@(2) �����Łu�����n�v�ł̉^���������@�e�@���@�����@���g���� �@�@�@�e�@���@�����f�@�{�@����0�@�@�@�@�@�@(3) �ڍ����āA �@�@�@�����f�@���@�e�@�|�@����0�@�@�@�@�@�@(4) ������u�����x�n�v�̉^���������Ƃ݂Ȃ��Ɓ@�|����0�@���u�݂����̗́v�Ƃ��ēo�ꂵ�܂��B ���g�\���F�@�������ˁB��]�n�ł́A�@�|�Q���ց~���@�|���ց~�i�ց~���j�@�ƂȂ��āA�ŏ��̍����R���I���́A�Q�Ԗڂ̍������S�͂ƌĂ킯���B �z�[���Y�F�@�����ł��B ���g�\���F�@�����ł��A���ɂȂ�̂�(4)���̍��ӂɓo�ꂷ��@�����f�@���B����͈�̉����̂��ˁB �z�[���Y�F�@�搶�̌����Ă���Ӗ���������܂���B ���g�\���F�@�u�����x�n�v����݂��u�݂����̉����x�v�ɕ��̂̎��ʂ��������ʂ��ˁB �z�[���Y�F�@�����ł��B ���g�\���F�@����ȗʂɂǂ�ȕ����I�Ӗ�������Ƃ����̂��B �z�[���Y�F�@�����I�@�E�E�E����������E�E�E�E�B ���g�\���F�@�u�����n�v�ł̉����x�́A�����^������̂���̑傫����]������Ƃ����Ӗ��ł��A���邢�͐^�́u�����́v�ɊW����ʂƂ��āA�����ʂƂ��ďd�v�ȈӖ��������A�u�݂����̉����x�v�͉��̈Ӗ����Ȃ��B�@ �@���۔C�ӂ̒l������ɐݒ肷�邱�Ƃ��\���B �z�[���Y�F�@�����ł��ˁB(1)���́@��0�@�ɂǂ�Ȓl��ݒ肵�Ă����܂�Ȃ��킯�ł�����ˁB ���g�\���F�@�t�������Č����A�K�����I�̑��ΐ��́u�����x�̒l�̔C�Ӑ��v�ł����āA�����x�ɂ��Ă͓��l�ȁu�����x�̑��ΐ��v���l���邱�Ƃ͂ł��Ȃ��B�@������A�u�݂����̗́v��t�������Ă����B �@��������O������B����́@���f�@���@�O�@�̏ꍇ���B���̏ꍇ�ɂ́A(4)���� �@�@�@�O�@���@�e�@�|�@����0 �@�ƂȂ邪�A�@���̏ꍇ�A���̂͊����n���猩�āA�@��0�@�Ŏ��ۂɉ������Ă���̂ŁA�܂�A�O�́@�e�@�Ɓ@�|����0�@�Ƃ��肠���Ă��鎮�A�܂�A�_�����x�[���̌����̎��ƂȂ�A�u�݂����̗́v�́u�����́v�Ƃ݂Ȃ��Ă悢���ƂɂȂ�B �z�[���Y�F�@���[��A�Ⴆ�Ώ�́u�l���n��������ꍇ�v�̂Q�Ԗڂ̐}�œo�ꂷ��u�n���̎�݂����̗́v�́A�n���́u�݂����̉����x�v�@���f�@�́@�O�@�łȂ�����A�����I�Ӗ��̂Ȃ��ʂȂ̂ł��ˁB����������Βn���ɂ���ȑ傫�ȗ͂������Ȃ�Ă��肦�Ȃ��ł��ˁB ���g�\���F �����ȂB�u�́v�Ɩ��Â�����ɂ́A�u�́v�Ƃ��Ă̕����I���̂��Ȃ���A�����ĂׂȂ��͂��Ȃ̂ŁA�����܂Łu�݂����́v�Ƃ����`�e�����t���킯���B �z�[���Y�F�@�悭������܂����B����Ɉ���₵�Ă����ł����B�@�搶�A���ꂶ��[�A�Ȃ������I�ȈӖ��s���́@�����f�@���܂�(4)�̎����g��ꂽ�肷��̂ł��傤���B ���g�\���F�@�����x�n�i���Ɏ��]����n�����j���猩�����݂̂̂����̉^�������������A�v�Z����̂ɕ֗����Ƃ������R���炾�낤�B �@�D�D�D�D����ȊO�́D�D�D�D�@�l�����Ɋ����̂Ɏg���邩�ȁB �z�[���Y�F�@�����B ���g�\���F �@���ꂩ��̋c�_�ŁA�i�X�Ƃ��̈Ӗ����������Ă���Ǝv����B �@�g���b�N�̂��˖������@���g�\���F�@�����ŁA�d�v�Ȃ��Ƃ��q�ׂ悤�B�@�Ȃ��u�j���[�g���͊w�v�ɂ����āA�����x�n�ł͂��߂Ċ����͂�o�ꂳ����̂��Ɖ]���ƁA������ƁA�\�����������A �u�_�����x�[���̉]���悤�Ɂ@�h�O�͂Ɗ����͂��ނ荇���Ă���̂ɉ�������h�@�Ȃ�Ă��Ƃ͋����Ȃ��B�@�����A���̂Ƌ��ɉ����x�^������ϑ��҂ɂ����͋����Ă�낤�B�@�Ȃ��Ȃ�A���̊ϑ��҂��ƕ��̂͐Î~���Č����邩��B�v �Ɖ]���킯���B �Ƃ��낪���ۂɂ́A�ʂ̃y�[�W�ŏq�ׂ��悤�ɁA���Θ_�I���ʂ������ł���͈͂ł́A�͂͊ϑ��҂̍��W�n�ɂ���ĕς邱�Ƃ͖����B�@ �@���Ƃ��� �O�̐}�T�ŁA�����Ă����q�ɓ����͂́A�n�ʂ���ɂƂ��Č���A�d�ԂɌŒ肳�ꂽ���Ȃɔw����������āA�O���ɉ���������ꂽ�Ƃ�������h�����R�́h�ł���A�܂���������d�Ԃ���Ɏ���Ă��A�����傫���̊����͂��B�@����ς��Ƃ���͂Ȃ��B �S���������������B�@��������������A�����x�n�ɂȂ�ƓˑR�����͂ƍl����̂͂������Șb����B �@�܂��A�~�^���̏ꍇ�ł��A�킴�킴�����x�n��o�ꂳ���Ȃ��Ƃ��A�n��̊ϑ��҂̗���ł��A�~�^���Ɖ]�������x�^���ɔ����h�����R�́h�i���~�̒��S�����ɉ^���ʃx�N�g���̌�����ω������悤�Ƃ���̂ɍR���銵���R�́j�Ƃ��āA�h���S�́h�������Ɣ������Ă���̂���B �z�[���Y�F�@�Ȃ�قǁA�����Ȃ̂��B����ƕ������Ă��܂����B �@�����x�n���g��Ȃ��Ă��A�����͂͂����Ƒ��݂�����B ���g�\���F�@��������A�@�킴�킴�g���b�L�[�ȉ����x�n�������o���āA�����͂̐�����������̂�����A���������A�����݂͂͂����̗͂��Ɖ]���h�G�ꂬ�ʁh�𒅂����邱�ƂɂȂ�B �z�[���Y�F�@�������I�@�@�@�ϑ��҂������x�n�Ɉڂ��Ă��A�h�{���̗́h�@�ł���@ �h�����́h�@�͑S���ς��Ȃ����̂Ȃ̂ɁA�@ ���������@�h�݂����̗��h�@�̂悤�ɕς�邩�̂悤�Ɏv�킹��A�@�h ���w�I�g���b�N�h�@�@�@�ɉ�X�͈����������Ă����Ɖ]�����Ƃ��B ���g�\���F�@���̒ʂ肾��A�z�[���Y�N�B �@�����͂��h�݂����̗́h�ɋU�����邽�߂ɂ́A�����n�̊ϑ��҂��猩���Ƃ��A�����͂́h�݂����̗́h�Ɠ������A���݂��Ȃ����Ƃɂ���K�v������B �z�[���Y�F�@�������A�h�g���b�N�h�Ɖ]�����A�h�y�e���h�ł��ˁB ���g�\���F�@�c�O�Ȃ���A�����]���Ă����������Ȃ��ȁB�D�D�D �@ �z�[���Y�N�ɂ��@�h�g���b�N�h �̉���@�����A�������̓z�[���Y�N�A�悭���̂��ƂɋC���t���Ă��ꂽ�B�@�@�o������A���̃z�[���y�[�W�̓ǎ҂ɂ��A���ꂪ������悤�ɁA�������Ă��炦�Ȃ����B �z�[���Y�F�@������܂����B�C���Ă��������B �@�}�ł��́h�g���b�N�h��������܂��傤�B �@�@�@ 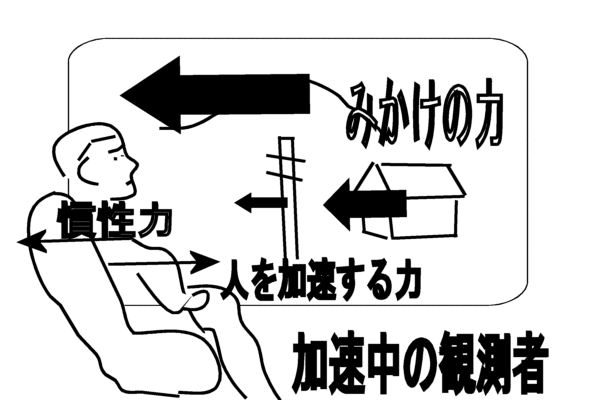 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�@�@�U ��̐}�́A�����x�^�����̗�Ԃɏ���Ă���ϑ��҂��猩���}�ł��B�����x�@���@�ʼn^������ϑ��҂���ɂƂ�i�������x�n�j�A���̊O�̂��ׂĂ̕��̂́A�|���@�̉����x�Ō�։^������悤�Ɍ����܂��B�@��������ʁ@���@ �̕��̂ɂ́A�[�����@�́h�݂����̗́h�����������߂��Ɗϑ��҂͉��߂���킯�ł��B �@�܂�A�n��ɂ���A�R�A��A�d���A�ƁA�D�D�D�D���₻�ꂾ���ł͂Ȃ��A�n�����g�A�S�F�����A�����̎��ʁ@���@�ɔ�Ⴕ���@�|�����@�́h�݂����̗́h�ɂ���āA�ϑ��҂̌���ցh�݂����̉����x�h�@�[���@�Ŕ��ōs���悤�Ɍ����܂��B �D�D�D�D�������Ă��鎩�����p���������Ȃ�܂����A�D�D�D�D����͂�S���A�h�݂����̗́h��h�����x�n�h�Ƃ����̂́h�g���f���h�Ȃ��@�㕨�ł��ˁB�@�D�D�D �@���ܗᎦ�������̂ɂ͂��ׂāA���ۂɂ͂����������͂������Ă��Ȃ��͖̂��炩�ł��B�@�@�������@�|�����@�̗͂̒��ŁA�܂Ƃ��ȗ͂�����܂��B�h���ۂɉ����^���h���Ă��镨�̂ɓ����h�����́h�ł��B�@�}�ł́A�ϑ��ҁ@�ɓ��������͂��������Ă��܂��A�������Ă����Ԃ̍��ȁA��v�A�D�D���A��ԑS�̂ɓ����A������́h�����́h�ł��B �����́A���ׂāA�ˌv��Ƃ��Z���T�[�ŁA���ۂɗ͂��������Ă��邱�Ƃ��m���߂邱�Ƃ��ł���{���̗͂ł��B �@�@�@�@�@�@ 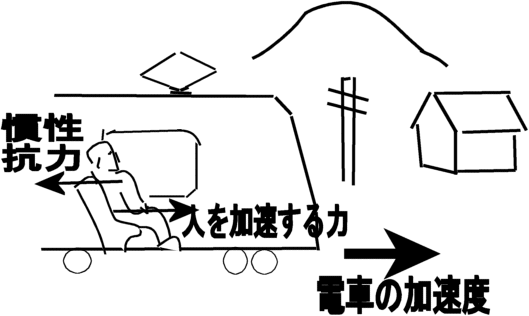 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�@�@�V �@���āA���q�ׂ��̂́h�����x�n�h�ł̘b�������̂ł����A���ɁA�h�S�����������h��Î~�n�i���h�����n�h�j�ōl���Ă݂܂��B�i��̐}�@�V�j ���x�́A�R�A��A�ƁA�d���A�D�D�D�͐Î~�����܂܁A�܂�����x�[���Ȃ̂ŁA��قǂ́h�݂����̗́h�͓��R�[���ɂȂ�܂��B �@����ɔ����A�����͂̕��͉���ς�炸�A���݂��܂��B�@���Ƃ��ΐ�قǂ̏�q�́A���Ȃɉ�����āA��ԂƋ��ɉ����x�^���������܂����A����ɋt�炤�h�����R�́h�Ƃ��Ĕ������܂��B�@����́A��قǂ́h�����́h�ƑS���������̂ł��B�@���̗͂́A���Ƃ��A���ȂƔw���̊Ԃ��h���́E�Z���T�[�h�����t������A�������͐��������̉��������͂̑����Ƃ��Ċϑ��ł�����̂ł��B �@���̂悤�ɁA�h�݂����̗́h�����ł��Ă��A�h�����́h�̕��͑S���ς��܂���B �܂�A�h�����́h�́h�݂����̗́h�ł͂Ȃ����Ƃ̓����ʏ؋��ł��B ���g�\���F�@���[��D�D�������̓z�[���Y�N�B�@���T��h�z�[���Y�h�̖��ɒp���Ȃ�������B �z�[���Y�F�@�G�w�w�A�D�D����قǂł��B ���g�\���F�@�h�݂����̗́h�̐����}�Ƃ��āA�z�[���Y�N�̎������h�}�@�U�h���ł��K�����B �@�����̉���ł́A�h�}�@�U�h�ƈقȂ�A�h�g���b�N�������邩�̂悤�Ɂh�A��������d�Ԃ́h�ԓ��h�̐}�i���Ƃ��A�킵�́h�����͂̕W���I�����h�̃y�[�W�̂�v�̐}���@�j���g���Đ���������̂�����A�h�݂����̗́h�͂��������h�����^�����Ă���ꏊ�i���ԓ��j�Ŕ������錻�ہh���ƍ��o�������Ă��܂��B�@���̌�����A�h�݂����̗́h�Ɓh�����́h�Ƃ̍����ށB �@�����ł͂Ȃ��A�h�݂����̗͂Ƃ͉�������ϑ��҂��猩�����ۉ����h�ł����āA�z�[���Y�N�̐}�@�U�@������A���̐��̂��A�h�����́h�Ƃ́A�h���Ĕ�Ȃ���́h�@�ł��邱�ƂɋC�Â����낤�B �@�܂��A���ׂẮh�{���̗́h�́h�ϑ��҂̉^���h�ɂ���č��E����Ȃ����ƁA�ϑ��҂𗣂�Ď��݂��邱�ƁA���Z���T�[���g�����c�_�ŋ������Ă��ꂽ�B �@�܂��A�}�@�U�@����@�h�Q���h�̗́@���Ȃ킿�@�h���̂�����������O�́@�Ɓ@���̂ɔ������銵���́@���@�t�����ő傫�����������h�@���Ƃ������邪�A����炪�@�}�@�V�@�̗͂Ɠ����ł��邱�Ƃ���A�@�t�ɁA�����n�ŁA�����W�A���Ȃ킿�@�h�_�����x�[���̌����h�����藧���Ƃ������Ă���B�@�h�_�����x�[���̌����h�̈Ӗ��́A��Ő������悤�B �@�����͐����𑽗p����̂ŁA����������ǂ��čs���Ɓh�����I���ρh�������Ȃ��Ȃ��āA�z�[���Y�N�̘b���Ă��ꂽ�悤�ȁA�펯�I�Ɂh�]���̂��p���������h���Ƃ����C�ŁA�咣���������B �@��ʑ��Θ_�Ɗ����́@���g�\���F�@�����͂̋c�_�ɂ́A���͖��Ȃ��Ƃ��܂��c���Ă���B�@�@�u��ʑ��ΐ����_�v���h���������h�@���Ȃ킿�@�h���W�n��ς��邱�Ƃŏd�͂͋Ǐ��I�ɂ͏������邱�Ƃ��ł���B�h�@�A�܂�@�h�d�͏�݂͂����̗͂̏ꂾ�h�@�Ɖ]�������@���咣���Ă���_�ɂ���B�@����������̌����̂P���B ��ɏq�ׂ��悤�ɁA�h�����́h�͊ϑ��҂̍��W�n�ɂ���ĕς��Ȃ��B�����瓙�������͂����܂Łh�d�݂͂͂����̗͂ł���h�Ɖ]���咣�ł����āA�h�����͂͏d�͂ł���h�Ɖ]���咣�ł͂Ȃ��B�D�D�D�D�Ƃ킵�͗������Ă���B�@��������݂͂͂����̗͂ł��Ȃ��B �z�[���Y�F�@�������A�����ȍ��Ȃ̂Ō���݂����ł��ˁB ���g�\���F�@�����ȂB�@���̏�A�Q�O���I���w�j���[�g���͊w�x�������͂������n�ł͈łɉB���āA����ɉ����x�n�œo�ꂳ����Ƃ����g���b�N���g�����̂�����A�݂�Ȗ�����Ȃ��Ȃ�B�@���ہA�킵���g�������������B �z�[���Y�F�@����ɁA�Q�O���I�������ȕ����w�҂̑������A�����͂̂��Ƃ��u�݂����̗́v���Ɖ]���Ă��܂����ˁB ���g�\���F�@�z�[���Y�N�A�����Ȃ�B�@�N�̉e�����m��Ȃ����A�܂��������������̂��B�@�F�A���ЂɎア����A�����v���Ă��܂��B�D�D�D�@�@�u�����́v�Ƃ́h�����R��( ������R �j�h�̂��Ƃł����A��قǂ́i�S�j���́@��0�@�̒l��ς���Ǝ��݂ɒl��ݒ�ł���A���Ȃ����̂悤�ȁu�݂����̗́v�Ƃ͋�ʂ��Ďg���ė~�����Ǝv���̂����B�D�D�D�@�������A�]���}�[�t�F���g��n�C�g���[�̂悤�ɁA�킵�Ɠ����Ӗ��Łu�����́v���g���Ă���L���Ȋw�҂����邪�B�E�E�E �@�@�z�[���Y�N�A�킵�̌����Ă��邱�Ƃ́A�Ԉ���Ă���Ǝv�����ˁB �z�[���Y�F�@�搶�̋��Ă�������������ƁA�ڂ����v���܂���B�@�@�g���b�N�ɂ��܂���Ă������ƂɁA���A����ƋC���t������ł�����B ���g�\���F�@���������A�P�Ȃ���W�ϊ������ŏd�͂Ƃ����A��K�͂ȗ͂��ȒP�ɔ�������Ȃ�āA�ǂ��l���Ă��M�����Ȃ��B �z�[���Y�F�@������A�������̗͂��Ǝ咣���Ă���킯�ł��ˁB�@�D�D�D�������A�h���������h���A�ʂ̈Ӗ��A���Ȃ킿�A�h���W�ϊ����s�����ƂŁA�Ǐ������n���K���̂��h�Ɖ]���Ӗ��ɉ��߂��邱�Ƃ��o���܂���ˁB ���g�\���F�@���ꂶ�Ⴀ�A�d�͂̑��݂��Ă���ꏊ�͊����n�ł͂Ȃ��A�{���͉������Ă��邱�ƂɂȂ�B �@�������l���Ă݂��܂��A�������Ƃ���A�d�͒��ŐÎ~���Ă���דd���q�́A�����^�����Ă���דd���q�Ɠ����Ƃ������ƂɂȂ�A���q�͐₦���d���g����o���Ă���͂�����B �i�@��l�ȉ����x�^���E�E�E���Θ_�̏����h�o�Ȑ��^���h�E�E�E�̏ꍇ�ɂ́A�d�����˂��N����Ȃ��Ƃ̌v�Z���ʂ�����悤�ł����B�D�D�j �z�[���Y�F�@���[��A�Ȃ�قǁA�D�D�D����ɁA���������A�d�͒��ŐÎ~���Ă��镨�̂ł��A���ۂ͉������Ă���Ȃ�A�G�l���M�[���ǂ�ǂ����邱�ƂɂȂ�܂���ˁB�@�t�ɃG�l���M�[���ς���Ă��Ȃ��Ȃ�A�����Ȃ��Ă��Ȃ��͂��B�D�D�܂��A�n�ʂ�������ɉ����^�����Ă���Ȃ�A����ɂ��鐯�Ƃ̋������ǂ�ǂ�k�܂邱�ƂɂȂ�܂���ˁB�@��ʑ��Θ_�ł́A���I�ȃ��[�N���b�h���������Ȃ��Ƃ̂��Ƃł����A�E�E�E���ꂶ��[�A�Ⴆ�A�n���ƌ��Ƃ̋����͂����炩�Ɖ]���c�_���ł��Ȃ��Ȃ��Ă��܂��B�D�D�D�悭�l����ƁA�������Șb����ł��ˁB ���g�\���F�@�@�m���ɂ������ˁB�@���̒n�ʂ́A���ۂɏ���������ʼn����^�����Ă���Ȃ�āA�M�����Ȃ���B�@������ƌv�Z����Ε����邱�Ƃ����A�P�N�Ԃ������ʼn��������Ȃ�A���Θ_�I���ʂ��l�����Ă��A�����ɋ߂����x�ɒB���Ă��܂���B�@���̒n�ʂ��I�I�D�D�D�D �@�u�A�C���V���^�C���̃G���x�[�^�v�i�����������j�͔�g�ɂ����߂��Ȃ��B�@�@�A�C���V���^�C�����_�́A�����܂ŁA����̌v�ʂɂ��Ă̗��_���B�@ �D�D�D�֑������A�L���ȑ啔�̈�ʑ��Θ_�̐�发�����@�i�D�k�D�@�r���������@�́A ���̖{�̏����ŁA�w�@�h���������h�́A���ɂ͑S�������ł��Ȃ��B�@���_�ݏo���h���Y�w�h�̖�ڂ��ʂ��������Ƃ͔F�߂邪�A���������A�ϑ��҂̉^���@�i�����������������f���@�����������|���������@�j �@�Ɉˑ�������̂��h�����h�Ƃ��č̗p���邱�Ǝ��́A�ԈႢ�ł���B�@�x�@�Əq�ׂĂ���B �@ �ނ͓Ǝ��̕��@���g�����h����̌v�ʂ̗��_�Ƃ��āh��ʑ��ΐ����_��_���Ă���B �@�܂��A���R���Y�����h���������h�ɂ��ẮA���l�Ȃ��Ƃ��q�ׂĂ���B�@ ���g�\���F�@ �@�����ȂƂ���A�u��ʑ��ΐ����_�v�́A�������^��_�̂��闝�_�ȂB �����������̂��̂������ɂ͐������Ȃ��B���Ƃ��Ύ���̋ȗ����������Ƃ��o���Ȃ��̂œd����̑��݂���ꍇ�A�����ɂ͐������Ȃ��i���R���Y�@���ΐ����_�E��g�@P162�j�B�@���������̂��߂�(����ʑ��ΐ��̉���̂��߂Ɂj�A�d�͏�̋Ǐ��G�l���M�[���A��ʓI�ɒ�`�ł��Ȃ��B�D�D�D���X�B �@���ɁA��̃G�l���M�[���Ǎ݉��ł��Ȃ��_�́A��̗��_�Ƃ��ẮA�v���I�Ȗ�肾�B �u���������v�̑��݂��d�̓G�l���M�[�̋Ǎ݉��������Ȃ��B �@ �@�����͈͂�ʑ��ΐ����_���瓱���Ȃ��B���g�\���F�@�@�@�������A��ʑ��ΐ����_���h���������h����b�Ƃ��Ă���̂ŁA �������������͂��d�͂Ɠ������̂ŁA�����͂͏d�͗��_�Ő����ł��邩�̂悤�ɍl����l�����邪�A �i�h���������h���������Ɖ��肵�Ă��j�A�����͋t�ŁA�@�d�͂̔����@�\����A�����͂̑��݂Ɉˑ����Ă���B �@���̊����̋N��������A�u�}�b�n�̌����v�������o���āA�����F���Ƃ̑��ݍ�p�̏��ׂɂ��Ă���B�@��ʑ��Θ_���j���[�g���͊w�����肷��u���ԁv�̖������������Ǝ咣���Ă��邪�A�u�}�b�n�̌����v���Ȃ킿�A �u�F���̎��ʕ��z�ŋǏ��I�Ȋ����n�����肳���v�Ƃ��邾���ŁA�u�j���[�g���̐��ԁv���u�}�b�n�̌����v�ɒu�������������ɂ����Ȃ��B �@�킵�� J.A.Wheeler�́u�����̋N���v�Ə̂���{���������Ƃ����邪�A�����͂̔����̃��J�j�Y���̐��������҂��Ă����̂����A �܂���������ꂽ��B �@�@���������A��ʑ��ΐ����_�����[����{���_�Ȃ�A���̊����͂̔����@�\����̋Ǐ��I���J�j�Y���Ƃ��Đ������ׂ����B �@�i�Ⴆ�A�d���C�͂̏ꍇ�A�ߐڍ�p�_�̓d���C�w�ł̓}�N�X�E�F���̉��̓e���\���ŁA�d���C�͂̋Ǐ������@�\������ł���B�E�E�E�E���̃��J�j�Y���͕ʃy�[�W�ʼn������\��ł��B�j�@ �@�����́i�������R�́j�̔����́@�d�͏�̗��_�@���瓱���Ă͂��Ȃ��B�@�Ǐ������n�ł̃j���[�g���̉^���������𗘗p���Ă���B�E�E�E�܂芵���͂𗘗p���Ă���ɂ����Ȃ��B�i�@�������A�d�͔����̃g���b�N�̂��߂ɁB�j �@��ʑ��ΐ����_���������Ƃ��A�������Ȃ��Ƃ��A����ȑO�Ɍ��R�Ƃ��āu�����́v�����݂���B �@�����āu�����́v�̓A�C���V���^�C���������������̂ł��A���_�Â������̂ł��Ȃ��B �@�ނ���A�����́i�������R�́j�͏d�͂ł͂Ȃ��A�h�j���[�g���̉^���������h�@�� �@�܂��A�����͂̍�p����p�̂Ƃ���ŏq�ׂ��悤�ɁA�h�^���ʕۑ����h�@�Ɩ��ڂɌ��т��Ă���B �@�����āA�A�C���V���^�C���������Ɋ֘A�t���Đ�������Ȃ�A�i���̎����������Ƃ��āj �@�@�@�@�@�@�@ 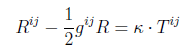 ���̉E�ӂɓo�ꂷ�������̃G�l���M�[�E�^���ʃe���\���i���̖��͌���ƍ�����^����B�@�������̓X�g���X�E�G�l���M�[�E�e���\���ƌĂԂׂ��ł���B�@���̂��Ƃɂ��ẮA�ʃy�[�W�ʼn���\��B�j�̔��U���[���ƂȂ邱�ƁA�܂�A�ʏ�̕����n���̃G�l���M�[�E�^���ʂ̕ۑ��@���@�ƊW���邾�����B �@���̍��ӂ̎���̋ȗ��ɊW����ʂƂ͖��W���B�@�@���������̗ʂ͌��Ⴂ�ɏ����Ȓl�ł���B �@������Ȃ��Ȃ�����A���̗�����ē����₻���B �@ �O�̃y�[�W�̐}���g���ƁA�L���b�`���[�̎�͂��h�d�́h���Ƃ��h�݂����̗́h���Ƃ��]���҂͋��Ȃ����낤�B �@�@�@�@�@�@�@�@�@�@�@�@ 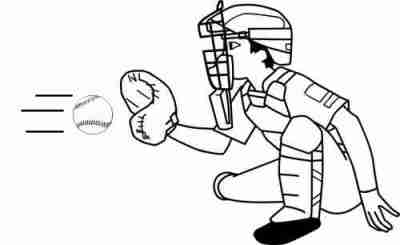 �@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�@�X �@�Ⴆ�͈������A���ɗ�Ԃǂ��������ʏՓ˂����đ厖�̂��N�������Ƃ��A��Ԃ���j���������́u�݂����̗́v�ł����Ė{���ɂ͓͗͂����Ă��Ȃ��A���Ƃ��A�u�d�́v�����������炾�A�ƌ�������A�S���u�������ꂵ���l�Ԃ��v�Ǝv���邱�Ƃ��낤�B �@�Ȃ��A�A�C���V���^�C���͊����͂��������̗͂��Ǝ咣�����̂��z�[���Y�F�@�@�������A�Ȃ��A�����͂��u�݂����̗́v���Ȃ�āA�N�ɂł����������Ǝv���邱�Ƃ��AEin stein ���͂��߁A�Q�O���I�̗D�ꂽ�����w�ҒB���C�Â��Ȃ���ł��傤�B�A���g�\���F�@�������ˁA�s�v�c���B �@�w�j���[�g���͊w�x�����ƂŘb�����j�I���R�ŁA�h�����́h�̑��݂��B�����B �@���Ԃ�A���ꂪEin stein�@�ɂƂ��čD�s�����B�@�Ȃ��Ȃ�@�B���ɉB���Ă��Ă����A��̂悤�ȁu�ʏ�̊����́v���������郁�J�j�Y������ʑ��Θ_�Ő��������ɍςނ���ˁB �z�[���Y�F�@�{���ł����B ���g�\���F�@�@���������A�h��ʑ��ΐ����_�h�́A�j���[�g�����h�����h���Ȃ킿�����n�̂��ƂɂȂ��ΓI�ɐÎ~������Ԃ�z�肵���̂��A�ے肷�邽�߂ɁAEin stein���\�z�������̂��B �@������A�����x�̒l�����߂��ΓI��͂Ȃ��B �@�Ⴆ�A�z�[���Y�N�́@�}�@�U�@�̗�Ԃ̉����x�̐�ΓI�Ȓl�͕�����Ȃ��B �@���������͂̑傫�������������I�ɑ���ł���B�@�ނ͂��ꂪ�h�d���h���ƍl�����B �@�܂�A�����x�̑���Ɂh�d����h�����݂���ƍl����킯���B�@������A�}�@�X�@�̃L���b�`���[�̎銵���͂��d�͏��������������ƂɂȂ�B �z�[���Y�F�@�Ƃ�ł��Ȃ����_�ł��ˁB ���g�\���F�@�������d�͈ȊO�́h��ʂ̊������h�ɂ͐G��ė~�����Ȃ������B �@�����̗͖͂{���A�h�j���[�g���̑�Q�@���i�^���������j�h�ƁA�h��p����p�̖@���h�ŏ������ׂ����̂ł���A�i�����̗͂ł͂Ȃ��j�h�������̗��h�ł���ƁB �z�[���Y�F�@���w�I�ɂ͂���ł悢�̂����m��܂��A�D�D�D���Ȃ��Ƃ������I�ł͂���܂���ˁB �@�@�h�ʏ�̊����́h�͞B���Ɍ떂�����Ă����āA�d�͂����́A�����́h�����́h�ł����H�H �@�@����͂Ȃ��ł��傤�I�D�D�D�B �@�@�D�D�D�������A���̘b�͖{���ł����B ���g�\���F�@���Ԃ�ˁB �@�킵���A����ɂ����z�������� �AEin stein �͔ӔN�܂ŁA��ʑ��Θ_����A�j���[�g���̉^�������������݁A�܂�u�ʏ�̊����́v���������w�͂𑱂��Ă������A �������A�������Ă͂��Ȃ��B �@�����͂̐[���Ӗ��@�@���g�\���F�@�Ƃɂ����A���̂悤�ɒʏ�A��X���o�����銵���͂́h�d�́h�ł��h�݂����̗́h�ł��Ȃ��B �h�����́h�́h�^���ʂ�^���G�l���M�[�̕��g�h�ŁA�t�ɁA�͊w�̒��S�I���݂��B �܂��A�h�_�����x�[���̌����h�̈Ӗ�������e���������Ă���B �@�͂̐ÓI�荇���ł͂Ȃ��A�O�͂ʼn����^������ۂ̉����x�ɑ��镨�̂���́h�����h���h�����́h�ŁA �@�����Ȃ�A�����́|�����́h�^���ʂ�^���G�l���M�[�̕ω��̑㏞�h�Ƃ��Č��ꂽ���̂��B �@���̌����́A �@�@�@�h�͊w���ۂł͊����͂�������I�o�����X�����藧���Ă���B�h �Ɖ]���Ӗ����B �@���́h�o�����X�h�͐ÓI�Ȓނ荇���ł͂Ȃ��A���x����́h�o�����X�h�ŁA�h���m�Ȏn���h���Ӗ����Ă���B�@���Ȃ킿�����x�^���̍ۂɁh�����͂���āA�G�l���M�[��^���ʂ𑼌n�����m���n�������h�����Ă���B �@�h�����͂��Ȃ��ƁA�^���G�l���M�[��^���ʂ̎n������o���Ȃ��B�h �z�[���Y�F�@���݂܂���A���Ă��邱�Ƃ������ς�A�킩��܂��B ���g�\���F�@�͊w�I�G�l���M�[�ۑ����Ɗ����͂̊W�̏ڂ����b�́A�ʃy�[�W�u�����͂ƃG�l���M�[�ۑ����v�ł�������A����܂ł��a�����B �@�Ƃ���ŁA�z�[���Y�N�B �@�܂��A���̊����͂́A���j�I�ɂ́A�j���[�g���̎���A��p�ҒB�����w�I�ɐ��������`�́@������w�j���[�g���͊w�x�����ɂ������āA��̂Ă�ꂽ�@�h�C���y�[�g�D�X�h�ł�����B �i�u�C���y�[�g�D�X�v�ɂẮA�ʃy�[�W�u�^���ɂ��ẮA�펯�T�O�v��Hestenes�̘_���i�o�c�e�j���Q�Ɓ@�j �������A�h�S��h�ł͂Ȃ����B�@�h���݂���́h���B�@�͊w���ۂ̍�����S���d�v�ȓ���������͂��B �@�����n�ŕ��̂������^������Ƃ��K���o�����Ă���ɂ�������炸�A���O���t���Ă��炦���A���Č��ʂӂ������Ă���B �����āA�����x�n�Ɖ]������ɁA����Ɠo�ꂳ���Ă��炦��Ǝv������A���킢�����ɁA�h�݂����̗́h�Ɖ]��������t�����A�h�������h��������������B�D�D�D�j���[�g���ȑO�͗͊w�̉Ԍ`�E����������̂ɁD�D�D�D�w���Ƃ������������ȗ��_�̋]���ɂȂ��ĂȁB�D�D �D�D���ɁA�s�����Ƃ͎v��Ȃ����B�@�z�[���Y�N�B�D�D �z�[���Y�F�@�搶�A�ǂ������ꂽ��ł����B ���g�\���F�@�n�n�A�n�n�D�D���܂�A������Ɗ����͂Ɋ���ړ����������悤���B�D�D �@���j�I�Ȏ����@���g�\���F�@�j���[�g���₻�̌�p�ҒB���h�C���y�[�g�D�X�h�E���悤�����̂́A�����́h�v�ٓN�w�I�Ȋw�h�A�܂�h���t�������g�����B���ȗ��_�h�ƌ��ʂ��邽�߂��B�@�j���[�g���̗L���Ȍ��t�Ɂ@�h���́A�����𗧂ĂȂ��B�h�@�����邪�A���́h�����h�Ƃ́A�h�Ȋw�Ɖ����h�̂���ł͂Ȃ��A�h�����h�܂�A���ۂ�������邽�߂ɍl���o�����ؖ����o���Ȃ��v�ٓI�Ȋw���̂��Ƃ��B�@�j���[�g���ȑO�̒����ł́A����Ȋw�����肪���𗘂����Ă��āA�ǂꂪ�������̕�����Ȃ��A�����̋ɂ݂������B�@�[�[�[���̃j���[�g���̌��t�͖��L���͂������郁�J�j�Y���ɂ��Ė��ꂽ�Ƃ��A�����̎v�ٓI�ȉ�����ނ��āA���w�ɗ��r��������̗����\���������̂ł���B�[�[�[ �@�h�B���Ȍ��t�h�ɑ���i�Ƃ��āA�ނ́h���[�N���b�h�w�h���܂˂āA�����A�藝����Ȃ��u�͊w�v����肠�����B �@�@�����A�e�D�x�[�R��������V�����h�����Ȋw�h���u�����Ă����B�����āA���̃T�[�N�����h�����h�����������h���B���̃����o�[�ł��������ނ́A�h���w�h�Ƃ����h���t�h���g�����ʂ̌`�́h�V�����Ȋw�h����肠���悤�Ƃ����B �@���̂��߁A�h�����I�h�ȊT�O���o���邾���킬���Ƃ����Ƃ����B�@�����]�����j�I�Ȏ���ŁA�ނ́A�����́h�C���y�[�g�D�X�L�h�̂���h�����́h�����_�ɓo�ꂵ�Ȃ��悤�ɍ�����ƁA�킵�͑z�����Ă���B�@���̏؋��ɑO�y�[�W�ŏЉ���悤�ɁA�v�����L�s�A�̖`���̒�`�W�ł́A���m�Ɂh�����́h�����݂��邱�Ƃ��j���[�g�����g�͔F�߂Ă������Ƃ������邪�B�E�E�E�E�@ �z�[���Y�F�@�����A�����ł��ˁB�@�@�����ǂނƁA�j���[�g���́A�h�����́h�����݂���̂��[���ɔF�����Ă������Ƃ�������܂��B�@����ɂ�������炸�A�����́h�C���y�[�g�D�X���h�ƌ��ʂ��邽�߂ɁA�܂��A�ނ�"�w�I�͊w�h�̘_���������т����邽�߂ɁA�����āh�����́h���̂Ă��Ƃ������Ƃł��ˁB ���g�\���F�@�j���[�g�����g�͂܂����m�ł͂Ȃ��������A���ɂ��̌�p�ҒB�����w�I�ɐ��������A������@�w�j���[�g���͊w�x�ł͂������B�@���̂��߁A�u�����v�̊T�O����A�������`�̊w�I�ȁu�����̖@���v�̂������ł����o�ꂵ�Ȃ��悤�ɂȂ��Ă���B�@�܂�A�O�͂����S�Ƀ[���̏ꍇ�Ɍ����������̖@���@�u�͂������Ȃ�����A���͓̂��������^���𑱂���B�v���B�@�͂��[���łȂ��Ă��A�^����ۂƂ��Ƃ���X���Ƃ��Ắu�����v�����݂���ɂ��W��炸�A�S������ɂ͐G��Ȃ��B �z�[���Y�F�@�����A�ȑO����A�ڂ������̂��Ƃ��s�v�c�ł��傤���Ȃ������̂ł����B ���g�\���F�@�G��邱�Ƃ́u�^�u�[�v�ȂB�@�Ȃ��Ȃ�A���̍L���Ӗ��ł́u�����v���������Ƃ���A���̂��Ɓu�����́v���o�ꂵ�Ă��܂����炾��B �z�[���Y�F�@�Ȃ�قǂˁB ���g�\���F�@������A�{���́u�����́v���o�ꂷ���ʂł́A������A�j���[�g���̑�Q�@���@�e�������@�̘b�ɒu�������āA�����͂�����킯���B �z�[���Y�F�@�m���ɁA�����x�^���̏ꍇ�́A�����͂��g�킸�ɁA����Ɂ@�^����������K�p���āA�������������͂������Ă��Ȃ����̂悤�ɁA���������x�^���Ƃ����A�u�^���w�I�v�A�搶�̕\���ł́u�w�I�v�Ȗ��ɂ���ς��Ă���킯�ł��ˁB �@����ŁA�u�����̖@���v�u�^���̖@���v���܂߂āA�͊w�̖�肷�ׂĂ��A�u�����́v��r�������A�u�w���v�ɒu�������Ă���̂ł��ˁB ���k�́h��T�O�h�͌�T�O�ł͂Ȃ����g�\���F�@�@���̒ʂ肾�B�@�������A���̎���ɂ́A�m���Ă��Ȃ������A�G�l���M�[�₻�̕ۑ����A�����āA�d���C�w�A��̊T�O�D�D���A�L���ȊT�O�i����͉����ł͂Ȃ��j�����܂ꂽ���̉�X�̎���ɁA�u�j���[�g���͊w�v���̖̂܂܁A�܂芵���͂������`�ŁA���Ȃ��Ȃ��g��������̂͂ǂ����Ǝv���̂����B�D�D�D�z�[���Y�F�@�m���ɁA�h�����́h�Ɋւ��ẮA�搶�̎w�E���ꂽ����������܂����ˁB ���g�\���F�@���̒ʂ肾�A���ꂪ�A���̕ʃy�[�W�Ŏw�E�����悤���A���������A�䂪�������łȂ��A���E�I�Ɍ��Ă��A�傫�ȏ�Q�ɂȂ��Ă���B�@�����A�قƂ�ǂ̋��t�́A���k�̌�F���E�h��T�O�h���Ƃ��āA�ʼn߂��Ă���B �@�������t�Ɛ��k�Ƃ̊��o�̂���̑傫�Ȍ����́A���̂��h���_�h�Ƃ����A�w�I�ȁh�_�h�ŕ\�킵�A�͂��h���u��p�h�Ƃ��āA�w�I�Ɂi�����̊Ԃ̑��ΓI�Ȉʒu�Łj���܂�͂Ƃ����@�w�j���[�g���͊w�x�̗��_�̏��ׂ��B �@���́h�w�I�Ȏ��_�h�Ɓh�w�I�ȗ́h���A�h�������o�h����V�������h���w�I�Ȓ��ې��E�h�֓����Ă��܂��B�@���ꂪ�A���t�������͂̑��݂ɂ��ē݊��ɂ��Ă��錴�����B �z�[���Y�F�@�Ȃ�قǁA�h���_�≓�u��p�h�ł́A�����͂��ǂ������Ă���̂��A���o�I�ɑS���݂͂悤���Ȃ��ł��ˁB �@���̓_�A���k�̕����A"�������o"�������Ă��܂�����ˁB ���g�\���F ���̒ʂ肾�B �@����ɉ����āA�h��p����p�̖@���h�𐔊w�������̂悤�ɁA����ȏ�l�@����K�v�̂Ȃ��A�j���[�g�������������A�h�A�v���I���Ȗ@���h�@�Ƃ݂Ȃ��Ă��邱�Ƃ���肾�B �@��p����p�̖@�����A�A���̂�}���̗́A���Ȃ킿�ߐڍ�p�̗͂ɗR�����邱�Ƃ�Y��Ă���B �@�����ƁA�����̘A���̂ɓ����Ă���͂͂���A�h�x�N�g���h�ȑO�́h�e���\���́h�Ƃ��Ắh�̖͂{���h��h�����͂̑��݁h�ɋC�t���͂��Ȃ��B �@�ȑO�ɏq�ׂ��A�ʃy�[�W�i�͂̓x�N�g�����H�u�ߐڗ͓���v�j�̐������J��Ԃ��ƁA �@�@�@ 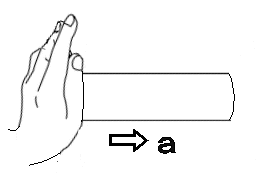 �@ �@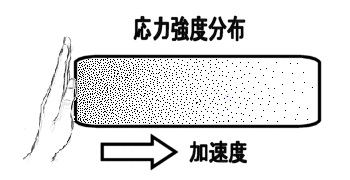 �@�@�@�@�@�@�@�@�@�@�@�@�}�@�Wa�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�@�W�� �@��ŕ��̂������āA��������ꍇ���l����Ɓi�}�Wa�j�A���̂Ƃ����̂ɂ́A�O�����牟���ꂽ�͂ɂ�蕨�̂��c�݁A�����ɉ��͂���������B�@���̉��͂͐}�W���̂悤�ɁA��ɋ߂����قǁA���̋��x�͋����A���Α��̒[�ɋ߂����قǎキ�Ȃ�B�����āA���̐�[�ł́@�O�@�ɂȂ�B�@����́A�Ȃ����Ɖ]���ƁA�����ɂ��A���̓��e�����ɉ����x�Ƌt�����Ɋ����͂������A�e���Ő}�@�X�@�悤�ɁA���͂Ɗ����͂̃o�����X���������邩�炾�B�i�@���@�́A�������@�`�@�̎��ʁ@�j �@�@�@�@�@�@�@�@�@�@�@�@ 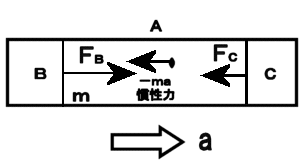 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�@�X �@�����ŕ����@A�@�ɒ��ڂ���ƁAA�@�̎�͂́A���[����̉��͂̍��@FB - FC �Ɓ@�����́@�|�����@�� �@�����̊ԂŁA�o�����X�i�_�����x�[���̌����j�����藧���Ă���B �@�@�@�@�@FB�@�|�@FC�@�|�@�����@���@�O �@���̌��ʁ@�}�@�W���@�̂悤�ȉ��͕��z��������킯���B �������A���̌��ʁA�}�@�W���@�̍��[�ŁA��̉������́@�e�@�Ɓ@���̂ɐ����������͂̑��a�@�|�l���@�i�l�͕��̑S�̂̎��ʁj�@�Ƃ��o�����X���Ă��邱�ƂɂȂ�B�@���̂悤�ɁA�����͂́A�����Ƒ��݂��Ă���B �@��̋c�_�́A�͂̊W������A�ϑ��҂��u�����n�v�ɋ��悤�ƁA���̂Ƌ��Ɂu�����^���v���ċ��悤�Ɛ��藧�B �@�܂��A���͂��e���̂̕ψʁi�ό`�x�j�ɔ�Ⴗ�邱�Ƃ��l����ƁA�}�X����A���I�Ȓe���̂̔g�����������ȒP�ɓ�����B �d�v�Ȃ��Ƃ́A �@�͂͊ϑ��҂̍��W�n�ɖ��W�ł���A�@�͕͂��̘̂c�̑傫���ő���o����h�q�d�`�k�h�ȗʁi���́j�ł���B �@�i�@�ڂ����́@�ߐڗ͂ɂ��Ă̕ʃy�[�W���Q�ƁB�j �ȏ�̂��Ƃ���A �@�@���t���A�����͂��@�h�P�Ȃ锽��p���h�@�ƕЂÂ��āA���C�ł����Ƃ���A����͂ނ��땨������̔��Ȃ��ׂ��d�v�ȉۑ�Ɖ]���邾�낤�B ���g�\���F�@�@�����A���̏�Q�́A���t���A�ꌾ�A �@�@�u���ۂ́h�����́h�͎��݂�����A�w�j���[�g���͊w�x�ł́A�^���������𗧂Ă�ɂ������ẮA���ڂ��Ă��镨�̎��g�ɐ�����h�����́h�͖�������h���[���h�ɂȂ��Ă���B�v �@�ƁA�����ɐ��k�ɐ�������A����������Ȃ��B�D�D�܂��A�����͂̐����ɁA�����x�n���킴�킴�����o���K�v���Ȃ��B�@�u�ϑ��҂������x�n�Ɉڂ邱�Ƃɂ��A�͕͂ω�����v�@�Ɖ]���@�h�R�h�@�������邱�ƂɂȂ��Ă��܂��B �@����Ȃ̂ɁA�ނ��ɂȂ��āA�h���S�́h�Ȃǂ́h�����́h�̎��ݐ���ے肵�āA�u�݂����̗́v�ł���Ƌ��ق��邱�Ƃ́A���m�ł�����A�^���ɍl���Ă��鐶�k�ɁA�h�����͓���āA������Ȃ����̂��h�A�Ǝv���錋�ʂƂȂ肩�˂Ȃ��B �z�[���Y�F�@�Ȃ�قǁB�m���ɂ��̒ʂ�ł��B �@�������A�����̊�{�@�����h���[���h�ƌĂԂ̂ɂ́A��R������܂��ˁB ���g�\���F�@�@�E�[���A�D�D�@�����͂������w�j���[�g���͊w�x�͑听���������߂����߁A���ꂪ��E�s�N�ȗB��̗��_�ł��邩�̂悤�Ɏv���Ă���悤�����B�@�@�������A���x�A�R�̒��ɓo�铹�͂P�{�ł͂Ȃ��A���ʂ������悤�ɁA�u�����́v���l���ɓ��ꂽ�ʂ̗��_�̌n�����݂���B �@���ꂪ�A��ŏq�ׂ�u��͗͊w�v���B �@������A�����͂�����̂́A�w�j���[�g���͊w�x�̃��[���ɉ߂��Ȃ��B �@���̏؋��ɁA�O�y�[�W�Ŏw�E�����悤�ɁA�Q���̂̏Փ˂ł́A����̕��̂̊����͂����邱�Ƃ͕s�\���B �z�[���Y�F�@�m���ɁA�ǂ̕����̋��ȏ���ǂ�ł��A�����P�ɁA�Փ˂��镨�̊Ԃɍ�p�E����p�̊W�����藧�u�ԓI�ȁh�傫�ȗ́h�������Ƃ��������Ă��Ȃ��āA���̗͂������錴���̐���������Ă��܂��B�@�����āA�����h�͐ρh�̌v�Z�Ɉڂ��Ă��܂��ˁB ���g�\���F�@�Փ˂̍ہA�o���̕��݂̂͌��Ɏ����ɐ����銵���͂�ɋy�ڂ��Ă���B���̂��ߏՓ˂̍ۂ̏ڍׂȐ����͏Ȃ�����Ȃ��B�@�����͂������j���[�g���͊w�́A���_�̌n�Ƃ��āA�s���S�Ȃ�B �@������q�̐��k�ւ̐����̕\�����}�Y�C�Ȃ�A�u���́A�h�j���[�g���͊w�h�Ɠ����ȁA�����͂��l�������ʂ̗͊w�̌n�������B�v�ƕt�������āA�h�_�����x�[���̌����h����ɂ����͊w�̌n�̑��݂k�B����������̂��A�悢�����m��Ȃ��B �@�@�h�_�����x�[���̌����h�@���ā@���g�\���F�@�Ƃ���ŁA���̃z�[���y�[�W�̓ǎ҂ɂ́A�킵�̌����Ă�����e���A�܂��ْ[�I�Ȏ咣�̗l�ɕ������邩���m��Ȃ��̂ŁA�V�k�S�Ȃ���A�����ŁA�A�ꌾ�t�������Ēu�������B�z�[���Y�F�@�����A�������Ă��������B ���g�\���F�@�܂����ɁA�_�����x�[���̌����̎��@�e�|���� �� �O�@�Ɓ@�j���[�g���̉^���������@���� �� �e�@�Ƃ́A���̏�ł͑S�������Ȃ̂ʼn^�����v�Z�����ł͕ς��Ȃ��B �i���Ȃ݂ɁA�ϕ��������瓱����郉�O�����W���̕������́A�O�҂ɑΉ�����B�j�@�����A���҂̎��̉��߂��قȂ邱�Ƃ��B �@�j���[�g���̉^���������ł́A�h�͂ɂ��ǂ̂悤���^�������܂��̂��h�A�ɒ��ڂ���̂ɑ��āA�_�����x�[���̌����ł́A���́h�^���̍ہA�ǂ̂悤���͂̊W���������Ă��邩�h�ɒ��ڂ���B �@���̏ꍇ�A���̂ɐ���������x �� �̒l���ǂ����Č��܂邩�Ɖ]���ƁA�u�O���e �ƁA���̂ɔ������銵�����|���� ���t�����ő傫�����������Ȃ�悤�Ȓl�@���@�ɒB����܂ŕ��̂����������B�v �Ƃ������Ƃ��B�i���̈��ʂ̏��Ԃ͒P�ɕ�����Ղ����邽�߂̐����ł���A���ۂɂ͓������u���ɉ����^�����N����B�j�@�܂��A�����x�^���������N�����̂́A�����܂ŊO�͂����ł���A�����͂͂��̉���������A�ÓI�ȗ͂̒ނ荇���ł͖ܘ_�Ȃ��B�@�@������͂̒ނ荇���͊����� �|���� ���[���A�i�܂�����x�@���@���[���j�ŁA�O�́@�e�@�̘a���O�@�̏ꍇ�ł���B �@�܂��A�O�͂��ނ荇��Ȃ��ꍇ�ɂ́A ������h�₤�h�悤�������͂̔�����������^�����N����B �@����́A�h�̘͂A�����h��@�h��p����p�̖@���̈Ӗ��h�@�Ɩ��ڂɊW���Ă���B���@�ʃy�[�W�h�ߐڗ͂ɂ��āh���Q�ƁB �@�܂�A�@�O�͂̃A���o�����X���^���ʕω��ɓ]������Ƌ��ɁA�����͂̔����ɂ��A�͂̃o�����X��ۂ��Ă���B�@ 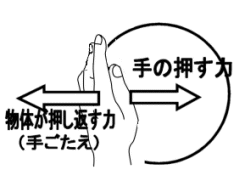 �@�_�����x�[���̌������A�����Ɗ��o�I�ɗ�������ɂ́A�O�y�[�W�ɋ������}�i�E�̐}�j���K�����B�@�@�����A�͂������鑊�肪�{�[���łȂ��āA�y���@�h�̂��h��������A�͈�t�������Ƃ��o���邾�낤���B �@�_�����x�[���̌������A�����Ɗ��o�I�ɗ�������ɂ́A�O�y�[�W�ɋ������}�i�E�̐}�j���K�����B�@�@�����A�͂������鑊�肪�{�[���łȂ��āA�y���@�h�̂��h��������A�͈�t�������Ƃ��o���邾�낤���B�z�[���Y�F�@��������͂̎�����ł��A�h�̂��ɘr�����h�̂��Ƃ��ʂ�A������撣���Ă��傫�ȗ͂͏o�܂����B ���g�\���F�@�ǂ����āA�o�Ȃ����Ƃ�������̂��ˁB �z�[���Y�F�@�E�}�́A�育�����i������p�j���قƂ�ǁA�Ԃ��ė��Ȃ�����ł��B ���g�\���F�@�������ˁA�܂�A��X�͌o������A�u���ۂɏo�����͂̑傫�����育�����̑傫���v�@���������邱�ƁA�܂�@�u��p�E����p�̖@���v�@��m���Ă���B�@���́h�育�����h�܂������R�́@�Ɖ���������O�͂��t�����ő傫�������������A���Ȃ킿�h�_�����x�[���̌����h�͉�X�̌o������f���ɗ����ł��邱�ƂȂ�B �z�[���Y�F�@�Ȃ�قǂˁB ���㕨���w�̊�b�́h�_�����x�[���̌����h���N�����g�\���F�@�Ƃ���ŁA�z�[���Y�N�A���㕨���w�̊�b�͗ʎq�͊w�����A���̗��_�́A�j���[�g���͊w���甭�W�������̂Ɖ]���邩�ˁB�z�[���Y�F�@�E�[���A�����Ƃ��]���܂����A�D�D�D�������A�ނ����͗͊w�ł��傤�ˁB ���g�\���F�@�������ˁA�ʎq�_�͂��ׂāA��͗͊w�I�T�O��p���ĕ\������Ă���B �@���̉�͗͊w�̊�b���n�~���g���̕ϕ������ŁA������u�_�����x�[���̌����v���u���z�d���̌����v����A�܂�A�u�^���͏�ɊO�͂Ɗ����͂��o�����X�����A���t��ԂƂ��Ď�������v�Ɖ]����������A���܂ꂽ���̂��B�@�����āu�j���[�g���͊w�v�̒P�Ȃ鉄���ł͂Ȃ��B �z�[���Y�F�@�������A���㕨���w�́A�u�j���[�g���͊w�v�ł͂Ȃ��A�����͂��܂ށu�_�����x�[���̌����v����b�ɐ��܂ꂽ�̂��B ���g�\���F�@������A�킵�̍��܂ł̋c�_�͌����Ĉْ[�I�Ȃ��̂ł͂Ȃ����Ƃ������邾�낤�B�@�ނ���A���㕨���w�̒��n�̐�c�̘b���B�@ �@�܂��A��͗͊w�ł́A�_�����x�[���̌����Ɖ]���h�͂̕��t����h����b�ɂ��Ă��邩��A�������W�Ɍ��炸�A�C�ӂ̋Ȃ������h��ʉ����W�h�ł��h���z�d���̌����h�����藧�킯�ŁA���ɕ������̂ł́A�i�j���[�g���͊w�̂悤�ɓ��͂��l�������ɁA�j�n�̎��R�x�ɑΉ������h��ʉ����W�h�����ɉ^���������𗧂Ă���B�Ⴆ�A�h�͂��ݎԁh���ɂƂ�A��]�p�Ƃ������R�x�ɑΉ������c�_���ł���B���Ȃ킿��]�́u�����v���Ƃ��A��]�́u�����́v�Ƃ����f���Ɉ�����B �z�[���Y�F�@�Ȃ�قǁA�͂��ݎԂ́A��x���n�߂�ƒ��X�~�܂�Ȃ��ł�����A�m���Ɂh�����h�������Ă���Ɖ]�������ł����A�w�j���[�g���͊w�x�ł́A�͂��Ȃ��ʼni���ɉ�葱���Ă��A�u��]�^���̊����̖@���v�Ƃ͉]��Ȃ��ł��ˁB ���g�\���F�@��������A���k�ɂƂ��ẮA�����^���̊����̖@�����A�͂��ݎԂ̊����̕�������݂�����A�f�����������₷���B�@�����̈Ӗ�����蕪����Ղ��Ǝv���B�@���̓j���[�g�����g���u�����̖@���v�̐����ŁA��]��������u�R�}�v���ɋ����Ă���̂��B�@�������A�w�j���[�g���͊w�x�ł́A�u�����̖@���v���^���݂̂Ɍ��肵�Ă���̂ŁA�c�O�Ȃ���A�������̗�Ƃ��Ď��グ���Ȃ���B�D�D�D �@ �@�܂��A��͗͊w���L�͈̗͂͊w���ۂɓK�p�ł��邱�Ƃ���A�t�ɁA�͂̕��t��Ԃ̌����i�������͂̑��݂ƃ_�����x�[���̌����j���A���R�E�́h�^���h�ł������Ƃ������邾�낤�B �@��͗͊w�́A���z�d���̌����̊g���ł����u�ϕ������v���g�����A�G�l���M�[�̌����@���Ȃ킿�A�Q��̗́A�����͂ƊO�́i�|�e���V�����́j�Ԃ̃G�l���M�[�̂����Ɋւ���G�l���M�[�ۑ����@���g���������R�x�n�̗͊w�ł���B �@���O�����W�����@�k�@���@�s�@�i�^���G�l���M�[�j�@�|�@�@�u�@�i�|�e���V�����G�l���M�[�j�@�ƂȂ�̂́A���̗��ҊԂ̃G�l���M�[�̂��Ƃ���ύt�i�o�����X�j��\�����邩�炾�B�@�@ �@�P��̃X�J�����ł��郉�O�����W�����ł͂��邪�A���z�ψ����g�����Ƃɂ��A�����R�x�̗͊w�n��������B�@ �@�d�v�Ȃ��Ƃ́A�h�����͂ɑ���d�����^���G�l���M�[�Ƃ��ĕۑ�������h�B�@�܂�A���Ԑϕ����l����ƁA�����͈͂��̕ۑ��͂Ƃ݂Ȃ������Ƃ��B �@�i�����ɂ��ẮA�ʃy�[�W���Q�����ĉ������B�j �@����炪������Ɠ���Ǝv�����͗͊w���A�����ł���悤�ɂȂ�B �@�t�ɉ]���A��p�ϕ��̕ϕ����[���ɂȂ�Ɖ]���h��p�����h���A���������_��I�Ȗ@���Ɏv����̂́A�_�����x�[���̌������[���ɗ������Ă��Ȃ��������B �@�����͂������`���I�ȁw�j���[�g���͊w�x�ŁA��͗͊w�����߂��悤�Ƃ���̂́A����������B �@�������A�c�O�Ȃ����͗͊w�̋��ȏ��̒��҂ł����A�u�_�����x�[���̌����v�ɔ��M���^�ŁA�P�ɂ����l����Ɠs�����悢�u�X�I�Ȍ����v���ƍl����n�����B�@���̂��߁A�������S�������ɍS�D���A�f�J���g���W�����ʉ����W�̃��O�����W�����������̂ɁA����ȘJ�͂��₵�Ă���B �@�_�����x�[���̌������u�͂̕��t��Ԃ̌����v�ł���A�u�����͂��^���G�l���M�[�ɑΉ�����ۑ��͂ł���v���Ƃ���������A�ȒP�ɗ����ł���b�Ȃ��B�E�E�E �@�͊w�͉�͗͊w�̒a���ɂ��傫���i�������ɂ��ւ�炸�A���{�̊����͂̎��ݐ����L���F������Ă��Ȃ��͕̂s�v�c���B �@����̉�X�͕������ۂ����������A���w�I���E�ɂ����錻�ۂ̂悤�ɑ����āA�ȑO�ɂ������āA���`�����E�d�������Ă���B�@���̂��߁A���w�I�ɕ\�����ꂽ���̂́A��̉��Ȃ̂��B�₦���u�����I�Ɂv�ǂ����߂���悢�̂����l����w�͂���X�ɋ��߂��Ă���B�@�����ƁA�u�����I���ρv��{���A�P������w�͂��K�v���낤�B �@��͗͊w�̉���͍������߂Ă��邱�Ƃɂ��āA�����ł́A����ȏ�̐����͂�߂Ă������B �z�[���Y�F�@�E�[���A����b�ł��ˁB ���g�\���F�@�@�b�������I�ȗ͊w�ɖ߂��ƁA�����͂������h�j���[�g���͊w�h�ł͉^���ʂ�͊w�I�G�l���M�[�̕ۑ����𐬂藧������A�d�v�Ȋ�{���J�j�Y���������Ȃ����Ă���B�D�D�D�D�D����I�ϓ_����́A���̎��̕������d�v���B �@����ɂ��āA�b�������̂����A�����͒x���̂ŁA�����͕ʂ̋@��ɂ��悤�B (�ʃy�[�W�́@�u�����͂ƃG�l���M�[�ۑ����v�@���Q�Ɖ������B�j �z�[���Y�F�@���[�ށA�c�O�ł����A������������܂���B�@���ꂶ��[�A������y���݂��Ă��܂��B �@�����͒����ԁA�l�̎���ɂ������Ă��������ėL��������܂����B�@��ϕ��ɂȂ�܂����B ���g�\���F�@�킵�̕����A�z�[���Y�N�̂������œ��̐������ł�����B �@�@�@�@�@�@�@�@�@�@�@�@�@���̃y�[�W�̃g�b�v�ց@ |
���������E�������珘�_�E��������̃y�[�W�̉�� �E�����͂ɂ��āi�����͏����j �E�����݂͂͂����̗͂ł͂Ȃ��B�i�����͑��ҁj�X�V �m�d�v�I �R���I���̗݂͂͂����̗͂��H�@�i�����͑Θb�@�Q�@�j �m�d�v�I �����͂ƃG�l���M�[�ۑ����i�����͑Θb�R�j �@�@�m�����I �E�G�l���M�[�̔����Ɓ@�ؓ� �E�͂̓x�N�g�����H�i�͂̐��̂�������B�j �E�͊w�n�Ƃ��Ă̓d���C�w�i�l�D�v�����N�́u���_�d���C�w�v��ǂށ@�m�d�v�I �E�J���[�ʼn��g�͂ǂ̂悤�ɔ��˂��Ă���̂��B �E�����h�f�f�e�X�g�h�Ɓh�^���ɂ��Ă̏펯�T�O�h ���������E�V�����́u�^���@���̎����v
�����z�� |