 |
|
| トップ物理教育情報教育ＧＰＳ考古学 | |
 力はベクトルか？（力の正体をさぐる）学校で「力はベクトルである」と習った人が多いかと思います。 しかし、本当でしょうか？ この私の問いかけの意味が理解できないかも知れませんので、以下にいくつかの質問をしますので、考えてみてください。 問１ 下の図のようにロープの両端をもって強く引っ張った。当然、ロープ中には力がみなぎっているはずです。ロープの途中で働いている力をベクトルとして表しなさい。またこの力の向きは右向きですか、それとも左向きですか。それとも力はゼロなのでしょうか。 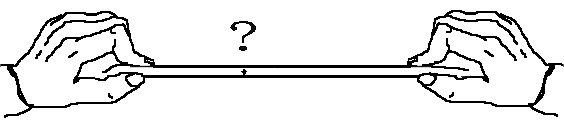 問２ 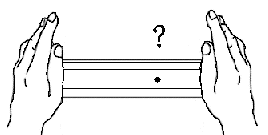 右図のように硬い棒を両側から強く押した。棒の途中の１点に働いている力をベクトルで同様に表しなさい。この力の向きは右向きですか、それとも左向きですか。それとも力はゼロなのでしょうか。 問３ 分厚い本があります。この本を机の上に置き、本の上から力 Ｆ で押しました。本の各ページには上から図のように各々全圧力 Ｆ が掛かっているはずです。この力が足し合わさると大きな力が机にかかる（１００ページの本なら１００倍の Ｆ の全圧力になる）はずですが、そうはならないのはなぜでしょうか。 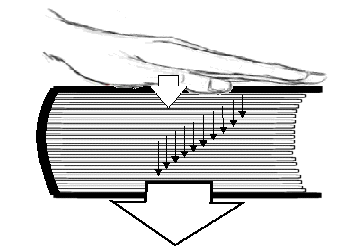 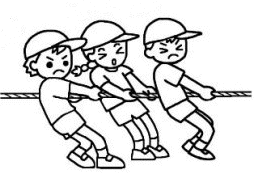 問４もし問３で、それらの力を足し合わすことが間違いなら、綱引き競技で、参加した大勢の人の出した力を足し合わす（赤組なら赤組全員の出した力の和を考える）のは間違いなのでしょうか。 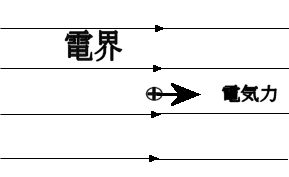 問５右は一様な電界中に置かれた正電荷が電気力を受けているようすを表した図です。この図は正しいでしょうか？ 応力としての力まず、上の問１、問２を例に考えて見ることにします。問１の場合にはロープがぴんと張っている（ロープが延びて変形を起こしている）はずです。 問２の場合は棒が押し縮められて変形しているはずです。そのためにそれぞれ内部に「緊張がみなぎっている」わけですが、それが実際の力の正体です。 これらは、右向きとも左向きとも言えません。当然向きを持つベクトルでは表せない状態です。 そしてこれらの「緊張」がロープ、あるいは棒の全体に伝わって（広がって）います。 こう言う「緊張」を物理では「応力」と呼んでいます。それではこの「応力」をどう表現すればよいのでしょうか。 そのためにひもや棒をいくつかの部分に仮想的に分割して考えることにします。 問１の例で考えると、ロープの途中で仮想的な面を考え、この面を境にロープを２つの部分ＡとＢに分けて考えて下さい。（実際にカッターでロープを切ったと想像して下さい。ただし、切ってそのまま引っ張ると離れてしまいますので、切り口を接着剤で再度つなぎ合わしたと考えて下さい。） 作用・反作用と向きをもつ面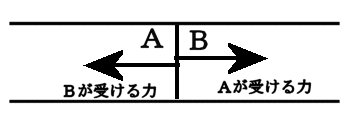 Ａの部分からＢの部分へは（Ａが受ける力を考えると）張力ですのでＢから右向きに引っ張られているはずです。逆にＢの部分からＡへは（Ｂが受ける力を考えると）へＡから左向きに力を受けています。 この２力は大きさが等しく向きは逆です。実はこの関係が正に「作用・反作用の法則」そのものです。すべての「作用・反作用の法則」はこの事実から導き出されます。 このように、緊張している媒体に仮想的な面を想定することにより初めて、「ベクトルとしての力」が現れてくるのです。 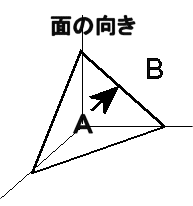 しかもこの面は「向きを持った面」であることに注意して下さい。通常、この面の向きはこの面に垂直な単位ベクトルの向きで表現することになっています。例えば、ＡからＢの向きに向いた面（Ａが受ける面）はその方向への単位ベクトルで表します。 Ａが受ける面は「Ａの表面に毛が生えている」と仮定して、その毛の向きと考えて下さい。 問１のような張力応力の場合は、この面に働く力（Ａが受ける張力）はＢへ向かうベクトルですから面の向き（Ａの毛の向き）とその面に働く力の向きは同じです。逆にＢからＡに向いた面（Ｂに生えた毛の向き）に働く力もＢが受ける力ですのでＢからＡへ向かうベクトルで、正の応力となります。 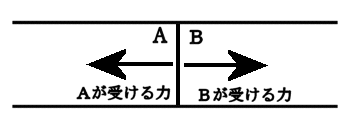 これに対して問２のような圧力応力の場合は同様な議論をすると、面の向きと逆向きに力が働いていることが分かります。例えば、ＡはＢから押されるのでＡの受ける面（Ａの表面の毛の向き）に働く力のベクトルは逆向きのＢからＡへ向きになります。（右図）つまり負の応力となります。 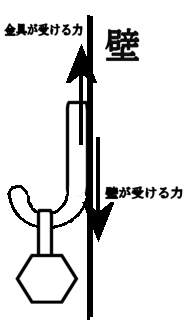 しかし一般には左の図のようにずれの応力と呼ばれる面の向きと応力の向きが平行でない場合もあります。ただし、壁面に垂直な応力成分は省いて図示している。 力はテンソルであるこのため一般的に応力を表現しようとすると、面の向きを表すベクトルを入力すれば、力のベクトルが出力として得られる「テンソル」と呼ばれる双線形量（入力、出力どちらもベクトルの重ね合わせの原理が成り立つ量）として数学的に定義されるのです。しかし物理的に注目して欲しいのは、逆向きの面ベクトルを入力すれば、大きさが等しく向きが逆の出力（力のベクトル）が得られることです。 つまり「作用反作用の法則」の数学的表現になっていると言うことです。 このことから、「力を数学的に表現するのに最も適した量は ベクトル ではなく テンソル である。」と言えます。 力の伝搬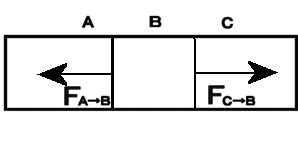 この応力は場所によって異なるのでしょうか。問１の場合で考えてみましょう。 今度は右図のように任意に２つの仮想断面を考えてみると、Ｂの部分は左右のＡ、およびＣから図のような力を受けていてそれらがつりあっているはずです。 つまり｜ＦA→B｜＝｜ＦC→B｜が成立しているので、任意の２つの断面での応力は等しいことが分かります。 つまり問１の張力はロープ中どこでも等しくなります。 我々は普通これを「力がロープの張力として伝わった」と表現しているわけです。 問２の場合も全く同様にして、棒の至る所で圧力としての応力は等しくなります。 これで問３の理由は分かりましたね。本の各ページの面を仮想断面と考えたら、単に力が圧力として伝搬しているわけで、圧力を足すことはナンセンスですね。 遠隔的な作用・反作用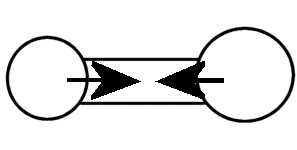 ここで「力の伝搬」と「作用・反作用」の関係に触れておくべきでしょう。そもそも「作用・反作用の法則」はニュートンが「遠隔力」の性質として述べたもので、私が上に述べた定義とは異なります。しかし、現代物理では「力はすべて場を介して伝わる」と考えられており、「瞬時に伝わる遠隔力」は有り得ないため、「作用・反作用の法則」は「近接力」でのみ成立します。 これは現在の物理学の立場でもあります。 しかし、応力を伝える媒質（＝力の場）の質量や、伝搬時間の遅れを無視した場合には力は媒質の端から端へ「遠隔力」として瞬時に伝わることになります。（上は端が２物体の場合の図） これが、２物体間での「遠隔力の作用・反作用の法則」とよばれているものです。 媒質の質量が無視できない場合を考えるためには、先に問４の綱引きの例を考察する必要があります。 綱引きについて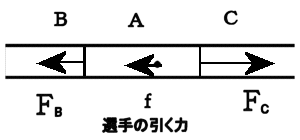 それでは、ここで問４の綱引きの場合を考えてみましょう。右は綱の一部分Ａに注目した図です。部分Ａは左側のＢから左向きの張力 ＦB を、右側Ｃからは右向きの張力 ＦC を受けています。 それらに加えてこのＡ部分にいる綱引き選手からの左向きの力 ｆ を受けています。 綱が動かない状態では、これら３力がつり合っているわけで、大きさで ＦC ＝ ＦB ＋ ｆ のつり合いの式が成り立っています。 つまり、右（前方）側の張力 ＦC の方が左側（後方）の張力 ＦB より、選手の出した力 ｆ の分だけ増えているのが分かります。 つまり、綱の張力は後方から前方へ進むにつれ、途中の選手が出した力の分だけ足されていくことが分かります。 この場合には張力は均質ではないのです。 つぎに媒質の質量が無視出来ない場合の力の伝搬について考えましょう。 慣性力と応力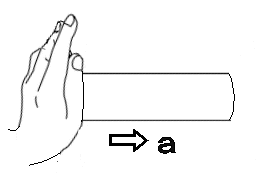 ここからは、動力学の話となります。今度は自由に運動できる棒の端に力を加えて棒を加速する場合を考えてみよう。（右図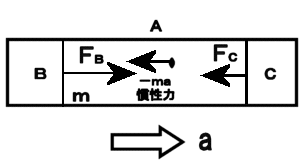）  この棒の一部分Ａに注目してみると、左側の部分Ｂから右向きに（全）圧力 ＦB で押されています。また、右側の部分Ｃから左向きの圧力 ＦC を左向きに受けています。 これら２力は等しくありません。なぜなら、途中のＡの部分は右向きに加速度ａで加速されているため、加速度と逆向きに「慣性力」を受けているからです。 慣性力の大きさは、Ａの部分の質量を ｍ とすれば、左向きに ｍａ です。 この力は綱引きでの途中の選手が出した力のように考えたら理解は容易でしょう。 結局、 ＦC と ＦB の大きさの関係は ＦC ＝ ＦB − ｍａ となりま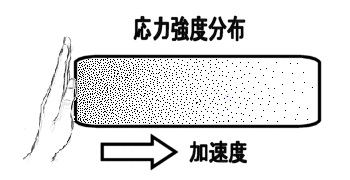す。  つまり、棒の右（前方）側ほど、応力は弱まっていきます。そして棒の右先端では応力は０となるわけです。つまり、媒質に質量があって自由に動けるとするなら、応力は途中の慣性力により変化しながら伝搬します。 右図の場合、左から右へ見ていくと、応力はあたかも慣性力のために吸収されていくように見えます。 これが、”新たな運動量が発生している”現場”の”力の様子”です。 逆に右から左へ見ていくなら、慣性力のため応力が新たに発生しているようにも見えます。 いずれにせよ、応力の端末（ターミナル）に慣性力が位置していることが分かります。（これが力学的な運動量やエネルギーへの転換を意味することを別ページで説明します。また電気力について似た例を説明する予定です。） また、慣性力は綱引きの途中の選手の出す力に相当し、現実に存在する力と言えるでしょう。 もし途中の力の媒質の質量が無視でき、媒質の反対側の端（図では左側）に質量のある物体が存在するなら、媒質の応力は反対端の物体まで伝わり、端にある物体の慣性力の所為で消費されます。（つまり、反対側の物体は反動で加速度運動します。この反対側の物体に働く慣性力がみかけ上、はじめの物体の慣性力の遠隔的反作用のようにみなすことも可能かも知れません。慣性力の作用反作用の法則をこの意味で使うなら、全系の運動量保存則と等価です。） 別の力の場が存在する場合たとえば、重力や電気力等の存在もそれらに対応する場の存在を仮定すれば、以上の議論を延長して考えることができます。電気力については私の別ページで問５の説明に関連して取り扱う予定です。 問５の説明はそれまでお預けにします。 |
物理教育・物理教育のページの解題・物理教育序論 ・慣性力について（慣性力序説） ・慣性力はみかけの力ではない。（慣性力続編）更新 ・慣性力についての対話( みかけの力とは？） 更新 ＮＥＷ！ コリオリの力について （慣性力対話 ２ ） ＮＥＷ！ 慣性力とエネルギー保存則（慣性力対話３） Ｎｅｗ！ ・エネルギーの発見と 筋肉 ・力学系としての電磁気学（Ｍ．プランクの「理論電磁気学」を読む） ＮＥＷ！ ・開口端で音波はどのように反射しているのか。 ・物理”診断テスト”と”運動についての常識概念” 物理実験・新方式の「運動法則の実験」
ご感想等 |